[ Article ]

Journal of Environmental Policy and Administration - Vol. 32, No. 4, pp.167-199

ISSN: 1598-835X (Print) 2714-0601 (Online)

Print publication date 31 Dec 2024

Received 01 Jun 2024 Revised 22 Sep 2024 Accepted 10 Dec 2024

DOI: https://doi.org/10.15301/jepa.2024.32.4.167

경제급전 모델을 통한 제주 목표 출력제어율 달성을 위한 대용량 ESS 최적 용량 산정

이성준^** ; 이주은^*** ; 박원빈^**** ; 윤설아^***** ; 김주연^****** ; 김도원^*******

**공동주저자, 부산대학교 산업공학과 연구원
***공동주저자, 부산대학교 산업공학과 연구원
****공동저자, 부산대학교 산업공학과 연구원
*****공동저자, 부산대학교 산업공학과 연구원
******공동저자, 한화오션 기계의장팀 기계제작사원
*******교신저자, 부산대학교 산업공학과 조교수

A Study on the Estimation of Optimal ESS Capacity for Target Curtailment Rates in Jeju through an Economic Dispatch Model

Seongjun Lee^** ; Jueun Lee^*** ; Wonbeen Park^**** ; Seola Yun^***** ; Juyeon Kim^****** ; Dowon Kim^*******

초록

제주의 탄소중립을 위한 재생에너지 설비 확대에 따라, 2030년에는 출력제어율이 약 19%까지 상승할 것으로 예측된다. 이를 해결하기 위해, 본 연구에서는 초고압 직류송전과 에너지저장장치를 고려한 혼합 정수 선형계획법 기반의 수리 모델을 구축하고 목표 출력제어율에 따른 에너지저장장치의 최적 용량을 산정하였다. 또한 발전기 출력 패턴 변화, 탄소 배출량, 발전 비용을 분석하였으며, 나아가 CFI 2030 목표에 부합하는 온실가스 감축을 위해 적절한 에너지저장장치 설비 투자 방안의 필요성을 제시하였다.

Abstract

With the rapid increase of renewable energy facilities in Jeju, the curtailment rate is predicted to rise to approximately 19% by 2030, and to address this issue, the study utilized High Voltage Direct Current (HVDC) and Energy Storage Systems (ESS). To that end, a mathematical model in the form of Mixed-Integer Linear Programming (MILP) was developed to determine the optimal ESS capacity under various target curtailment rates. Furthermore, this study examined changes in generator output patterns, carbon emissions, and generation costs with the findings underscoring the need for an effective investment plan in ESS facilities to meet the greenhouse gas reduction targets outlined in the CFI 2030 initiative.

Keywords:

Jeju CFI 2030, ESS Capacity Determination, HVDC, Cost Evaluation

키워드:

제주 CFI 2030, ESS 용량결정, 비용평가

I. 서론

제주는 2012년에 CFI 2030(Carbon-Free Island 2030) 정책을 시행하여, 2030년까지 재생에너지를 100%로 도입하여 탄소 제로섬을 구현한다는 에너지전환 계획을 발표하였다. 이 계획에 따라 산업통상자원부(2023)의 제10차 전력수급기본계획에서는 2030년까지 풍력 발전설비 용량 2,345MW, 태양광 발전설비 용량 1,299MW를 목표로 설정하였다. 그러나 태양광 및 풍력 에너지는 출력 조절이 어려우며 간헐성으로 인해 전력 계통의 부담을 가중한다는 문제가 있다. 이러한 문제로 재생에너지 설비를 대규모로 늘린다면 계통 안정도 저하를 발생시킬 수 있다. 이에 대응하기 위해 재생에너지 설비를 계통에서 떼어내 출력을 제한(Curtailment)하는 방식의 비효율적 수단을 사용해야만 하는 실정이다.

재생에너지의 간헐성은 전력 수요와 공급의 일치를 더욱 복잡하게 만들고, 운전 조건을 통제하기 쉬운 기존 발전기가 변동성 전원으로 대체되면서 유효전력 조정 능력이 줄어드는 문제를 일으킨다. 실제로 재생에너지 보급 확대에 따른 출력제한은 2020년에 77회, 2021년에 65회, 2022년에 132회 나타났으며, 현재와 같은 추세가 지속된다면 2030년까지 출력제어율이 19%까지 상승할 것으로 예상된다.¹⁾

이러한 배경에서, 2030년의 출력제어율을 완화하고 안정적인 전력 공급을 확보하기 위해서는 제주와 육지를 연결하는 초고압 직류송전(High Voltage Direct Current, HVDC)의 역송과 대용량 에너지저장장치(Energy Storage System, ESS) 설비 보급이 필수적이다. HVDC 정송을 통해서는 제주에 부족한 전력을 공급받을 수 있으며, 역송을 통해서는 제주에서 과잉 생산되는 풍력･태양광 전력을 육지로 송전하여 전력 수급 균형을 맞출 수 있다. 또한 신재생 발전기와 연계된 대용량 ESS 설비를 도입할 경우, 재생에너지 출력의 변동성을 완화하고 과잉 생산 전력을 저장하여 필요한 시간대에 공급함으로써 전력 수급의 안정성을 높이는 동시에 기존 발전기의 운행 변동 부담을 줄일 수 있다.

현재 제주에 설치된 HVDC #1, #2는 주로 전력 부족분을 제주로 공급하는 정송용으로 활용되고 있으나, 2023년까지 완공 예정인 HVDC #3²⁾를 비롯해 기존 HVDC #1, #2 역시 역송을 고려할 필요가 있다. 이를 통해 재생에너지 설비 용량이 증가함에도 출력제한을 최소화할 수 있는 효율적인 방법을 모색해야 한다. 따라서 HVDC #1, #2, #3의 운전 방식을 적절히 조합하여 재생에너지 출력제어율을 설정하고, 이와 함께 대용량 ESS의 최적 용량을 도출하는 과정에서 경제성을 동시에 고려해야 한다.

이에 본 논문에서는 혼합정수계획법(Mixed-Integer Linear Programming, MILP) 기반의 경제급전(Economic Dispatch) 모델을 제안하여, HVDC 운용 방식과 가격결정 발전계획을 반영함과 동시에 장･단주기 대용량 ESS를 고려할 수 있도록 하였다. 제안 모델을 통해 목표 출력제어율을 달성하기 위한 여러 시나리오를 시뮬레이션하며, 이에 따른 연도별 제주 지역 ESS 최적 용량을 산정하였다. 또한 최적 ESS 용량을 토대로 기존 발전기의 운전 패턴과 탄소 배출량 및 발전비용 등을 분석하여, 제주 CFI 2030 정책 달성을 위한 경제적･기술적 시사점을 제시하고자 한다.

Ⅱ. 선행연구

경제급전(Economic Dispatch) 문제는 전력 계통에서 발전단가, 전력 수요, 계통 제약 등을 고려하여 발전기 운용 계획을 수립함으로써 계통 운용비용을 최소화하거나 효율성을 극대화하고자 하는 핵심 연구 분야이다. 이 문제를 해결하기 위한 접근법으로 혼합정수계획법을 비롯해 동태계획법(Dynamic Programming), 유전 알고리즘(Genetic Algorithm), 입자군 최적화(Particle Swarm Optimization) 등 다양한 수리적･메타 휴리스틱 기법이 활용됐다.

예를 들어, Baldick(1995)는 MILP 기반의 경제급전 모델을 제안하여 전력 계통의 운용비를 최소화할 방안을 모색하였다. 구체적으로 발전기별 가동･정지 상태, 최소 운전 시간, 연료비 등을 세밀하게 반영함으로써, 전력 공급 비용을 단순히 줄이는 데 그치지 않고 계통 운영 안정성을 함께 고려하였다. 이어서 Mahmood and Al-Anbarri(2022)는 풍력 에너지를 계통에 통합할 때 발생하는 기술적･환경적 제약을 모델에 포함하고, 이 제약을 만족하는 선에서 전력 생산 비용을 최소화할 수 있는 전략을 분석하였다. 이를 통해 대규모 풍력 자원의 변동성을 반영한 경제급전 모델의 운용 가능성과 비용 절감 효과를 실증적으로 보였다.

다른 측면에서는 경제급전 목적함수에 탄소배출권 가격과 같은 환경 비용을 포함해, 환경 정책과의 상호작용을 다루는 연구도 이뤄졌다. 예를 들어, 김용건･구윤모･김동우･이원종･양유경(2019)은 온실가스 배출권 가격을 경제급전 문제의 목적함수에 추가하여, 배출권 가격이 상향 조정될 경우 발생할 수 있는 발전 포트폴리오 변화와 온실가스 감축 잠재력을 분석하였다. 이는 경제급전 문제에서 비용 최소화뿐 아니라 탄소 배출 저감 이슈가 점차 중요해지고 있음을 보여준다.

계통과 ESS의 연계 연구는 재생에너지의 간헐성을 보완하고 계통 안정성을 높이기 위해 경제급전 모델과 함께 주목받아 왔다. 백민규･박종배･손성웅･신하상･박용기(2018)는 태양광과 연계된 소용량 ESS를 대상으로, 신재생에너지 공급인증서(REC)를 고려하여 사업자가 최대 수익을 달성할 수 있는 최적 ESS 용량을 산정하였다. 다만, 해당 연구는 가격결정 발전계획(Pricing-based Generation Scheduling)을 고려하지 않았기에, 계통 운영자가 운용해야 하는 출력제어율 감소나 발전기 출력 변동률 최소화와 같은 공익적 측면보다는 사업자 수익 극대화에 초점을 맞추는 한계를 지닌다.

이에 반해, 대규모 ESS를 염두에 두고 경제급전과 가격결정 발전계획을 동시에 고려한 사례도 있다. 김병오･곽규형･김태현･신한솔･김욱(2021)은 두 단계 계획 문제(Bi-level Programming)를 통해 운영자와 ESS 사업자의 목표를 분리하여, 상위계층에서는 가격결정 발전계획을 수립하고 하위계층에서는 ESS 사업자의 이익을 최대화함으로써 최적 ESS 용량을 결정하였다. 또한 최윤석･나승유(2018)에서는 PCS와 ESS 최적 용량을 산정하여, 투자 비용 대비 수익을 최대화할 수 있는 운영 전략을 도출하였으며, 이 과정에서 다양한 시간대별 전기요금 체계를 분석하여 실제 운용 환경에 근접한 결과를 제시하였다.

HVDC 연계 연구 또한 경제급전 및 ESS 연계와 결합하는 방향으로 확장되고 있다. 그러나 국내외 학술 연구에서 HVDC와 대용량 ESS를 동시에 경제급전 모델에 반영한 사례는 아직 많지 않다. 예를 들어, Mich. et al.(2019)는 HVDC와 초고압 교류송전(High Voltage Alternating Current, HVAC)의 기술적 특성을 비교하여 HVDC 방식이 송전 효율 및 전력 품질 측면에서 우수함을 입증하였으나, ESS 통합 운용 방안은 다루지 않았다. 최근 연구로 Vatsal and Sharma(2023)가 HVDC 및 ESS를 포함한 다양한 전력시스템구성 요소를 통합 모델링하여 주파수 안정성에 미치는 영향을 분석하였으나, 이 역시 대규모 재생에너지 연계 ESS의 최적 용량 산정으로까지는 확장되지 못했다.

국내 사례로는 김자현･한가희･문희승(2022)에서 HVDC 역송용량을 고려하여 ESS 설치비용을 포함한 경제성 분석을 수행하고자 하였으나, 발전기의 최대 증감발량, 최소 운전 시간 등 세부 운용 제약과 장･단주기 ESS를 동시 고려하지 않아, 재생에너지의 출력을 장･단기간에 걸쳐 유연하게 대응하는 문제까지는 충분히 다루지 못했다.

본 연구는 이상의 선행 연구를 토대로, HVDC의 정송과 역송이 모두 가능한 환경에서 장･단주기 ESS를 함께 고려하고, 발전기 최대 증감발량･최소 정지시간･최소 운전 시간 등을 엄밀히 반영하는 경제급전 모델을 수립하고자 한다. 구체적으로 재생에너지 발전량의 변동성과 출력을 조정할 수 없는 특성을 경제급전 문제에 통합하여, 대규모 재생에너지 연계 ESS의 최적 용량을 산정하고 그에 따른 탄소 배출량, 발전비용, 그리고 계통 안정성 지표 변화를 체계적으로 분석한다. 이를 통해 대규모 풍력･태양광이 보급되는 미래 전력망에서 HVDC와 ESS를 활용해 안정적인 전력 수급을 달성할 방안을 제시하는 데 기여하고자 한다.

Ⅲ. 수리 모델

1. 목적함수

본 논문에서는 MILP의 최적화를 통해 결과를 도출하고자 하였다. 재생에너지와 재생에너지 연계 ESS를 반영한 경제급전 모델에서는 발전기의 운영에 따른 비용, HVDC의 운영비용과 ESS의 설치비용 및 운영비용을 고려하여야 하므로 재생에너지 연계 ESS 설치에 따른 전력 계통 운영에 드는 비용의 최소화를 목적함수로 선정하였으며 다음과 같다.

M i n i m i z e ∑ y ∈ Y ∑ t ∈ T ∑ g ∈ G G e n C o s t g, t, y + ∑ y ∈ Y ∑ t ∈ T H V D C C o s t t, y + ∑ y ∈ Y ∑ t ∈ T E S S C o s t t, y

(1)

G e n C o s t g, t, y = ∑ y ∈ Y ∑ t ∈ T ∑ g ∈ G H 1 × p g, t + H 0 × u g, t 2 × F C g 1 + d r y + O M g × p g, t 1 + d r y + S C g × v g, t 1 + d r y + C C × C g × p g, t 1 + d r y

(2)

H V D C C o s t t, y = ∑ t ∈ T, y ∈ Y h v d c t, y × H P 1 + d r y + h v d c t, y 졍 송 × S M P 1 + d r y

(3)

E S S C O S t t, y = E l C 1 × e 1 c T e n d + e 2 c T e n d 1 1 + d r y - 1 + E l C 2 × e 2 c T e n d 2 1 + d r y - 1 - E l C 1 × l i f e l o n g - Y + y - 1 × e 1 c T e n d + e 2 c T e n d 1 l i f e l o n g × 1 + d r Y - E I C 2 × l i f e s h o r t - Y + y - 1 × e 2 c T e n d 2 l i f e s h o r t × 1 + d r Y + P l C 1 × p 1 c T e n d + p 2 c T e n d 1 (1 + d r) y - 1 + P l C 2 × p 2 c T e n d 2 (1 + d r) y - 1 - P l C 1 × l i f e l o n g - Y + y - 1 × p 1 c T e n d + p 2 c T e n d 1 l i f e l o n g × 1 + d r Y - P l C 2 × l i f e s h o r t - Y + y - 1 × p 2 c T e n d 2 l i f e s h o r t × 1 + d r Y + E P 1 × p 1 c T [e n d] + p 2 c T e n d 1 1 + d r y + E P 2 × e 2 c T e n d 2 1 + d r y

(4)

식 (2)의 GenCost에서 $H 1 × p g, t + H 0 × u g, t 2 × F C g$ 는 발전기의 열효율 함수에 따른 운전 시 발생하는 비용을 의미한다. 열효율 함수는 2차식이지만 이를 1차식으로 간단히 하여 선형화하였다. OM_g×p_g,t는 발전기의 운영 비용을 의미한다. SC_g×v_g,t는 이진변수인 발전기의 기동 여부에 따라 발생하는 기동 비용을 의미한다.

식 (3)의 HVDCCost는 HVDC를 통해 제주에서 육지로 전력을 역송 및 정송 했을 때의 운영비용과 정송으로 받은 전력에 대한 비용의 합을 의미한다.

식 (4)의 ESSCost는 설치되는 재생에너지 연계 ESS의 총용량에 따른 비용, ESS의 설비용량에 따른 PCS의 설치비용과 ESS의 유지 보수 비용을 의미한다. ESS와 PCS 설비 설치에 대한 잔존가치를 고려하였다.

2. HVDC, ESS 및 전력수급 제약조건

태양광 연계 ESS 충전 및 방전 시간대 제약

e s s 1 t ∖ 24 = c ≤ 0, e s s 1 t ∖ 24 = d ≥ 0, ∀ t ∈ T, c ∈ c h, d ∈ d c

(1)

ess1은 단위시간이 8시간인 태양광 연계 장주기 ESS이고 ess2¹은 최소 충, 방전 지속시간이 4시간 이상인 풍력 연계 장주기 ESS이며 ess2²는 충, 방전 지속시간이 4시간 미만인 풍력 연계 단주기 ESS이다. 식 (1)은 태양광에너지의 충전과 방전에 따른 시간대를 적용하기 위한 조건이다.

태양광 연계 에너지저장장치 충전 조건

- v s t ≤ e s s 1 t - p 1 c t ≤ e s s 1 t, ∀ t ∈ T

(2)

풍력 연계 에너지저장장치 충전 조건

- v w t ≤ p 1 t e s s 21 - p 2 c t 1 ≤ p 1 t e s s 21 - v w t ≤ p 1 t e s s 22 - p 2 c t 2 ≤ p 1 t e s s 22 - v w t ≤ p 1 t e s s 21 + p 1 t e s s 22, ∀ t ∈ T

(3)

태양광 에너지저장장치 방전 조건

e s s 1 t ≤ e l 1 t e s s 1 t ≤ p 1 c t, ∀ t ∈ T

(4)

풍력 에너지저장장치 방전 조건

p 2 t e s s 21 ≤ e l 2 t 1 p 2 t e s s 21 ≤ p 2 c t 1 p 2 t e s s 22 ≤ e l 2 t 2 p 2 t e s s 22 ≤ p 2 c t 2, ∀ t ∈ T

(5)

식 (2), (3), (4), (5)는 충전 시에는 재생에너지 발전량과 재생에너지 설비용량보다 적게 충전하고 방전 시에는 ESS의 설비용량과 충전된 전력의 양보다 적게 방전하기 위해 설정하였다.

태양광 에너지저장장치 충전상태 조건

e l 1 t + 1 = e l 1 t - e s s 1 t e l 1 t ≤ e 1 c t, ∀ t ∈ T

(6)

풍력 에너지저장장치 충전상태 조건

e 2 l t + 1 1 = e 2 l t 1 - e s s 2 t 1 e l 2 t 1 ≤ e 2 c t 1 e 2 l t + 1 2 = e 2 l t 2 - e s s 2 t 2 e l 2 t 2 ≤ e 2 c t 2, ∀ t ∈ T

(7)

식 (6), (7) 는 ESS가 특정 시간에 충전 또는 방전한 양만큼 ESS의 전력 충전량 상태가 달라지기 때문에 특정 시간의 ESS에 충전된 전력량을 결정하기 위한 조건을 의미한다.

ESS 총 용량 및 설비용량 조건

e 1 c t + 1 = e 1 c t, p 1 c t + 1 = p l c t e 2 c t + 1 1 = e 2 c t 1, p 2 c t + 1 1 = p 2 c t 1 e 2 c t + 1 2 = e 2 c t 2, p 2 c t + 1 2 = p 2 c t 2, ∀ t ∈ T

(8)

식 (8)은 ESS의 총용량과 설비용량을 결정하기 위한 조건을 의미한다. 여기서 총용량은 ESS가 충전할 수 있는 전력 총용량을 의미하며, 설비용량은 ESS가 한 번에 충전 또는 방전을 할 수 있는 최대용량을 의미한다.

풍력 장주기 ESS 충‧방전 지속시간 조건

p 1 t e s s 21 + p 2 t e s s 21 = e s s 2 t 1 p 1 t e s s 21 ≥ - M × u 1 t e s s 21 p 2 t e s s 21 ≤ M × u 2 t e s s 21 u 1 t e s s 21 + u 2 t e s s 21 ≤ 1 ∑ t t = t + 1 t + min ⁡ (3, T e n d - t - 1) + 1 u 1 t e s s 21 ≥ u 1 t + 1 e s s 21 - u 1 t e s s 21 × min ⁡ 4, T e n d - t ∑ t t = t + 1 t + m i n 3, T e n d - t - 1 + 1 u 2 t e s s 21 ≥ u 2 t + 1 e s s 21 - u 2 t e s s 21 × min ⁡ 4, T e n d - t ∑ t t = 1 4 u 1 t e s s 21 ≥ u 11 e s s 21 × 4, ∀ t ∈ T

(9)

풍력 단주기 ESS 충,방전 지속시간 조건

p 1 t e s s 22 + p 2 t e s s 22 = e s s 2 t 2 p 1 t e s s 22 ≥ - M × u 1 t e s s 22 p 2 t 2 t s 22 e s s ≤ M × u 2 t e s s 22 u 1 t e s s 22 + u 2 t e s s 22 ≤ 1 t + min ⁡ 3, T e n d - t ∑ t t = t t u 1 t e s s 22 ≤ 3 t + min ⁡ 3, T e n d - t ∑ t t = t e s s 22 u 2 t e s s 22 ≤ 3, ∀ t ∈ T

(10)

식 (9), (10)에서 M은 충분히 큰 수를 의미하며, 충전 상태를 나타내는 $u 1 t e s s 21$ , $u 1 t e s s 22$ , 방전 상태를 나타내는 $u 2 t e s s 21$ , $u 2 t e s s 22$ 를 이용하여 각각 장, 단주기 ESS의 충, 방전 지속시간을 결정해 주기 위한 조건을 의미한다. 따라서, 장주기 ESS의 경우 최소한 4시간 이상을 충전 또는 방전하며, 단주기 ESS의 경우 최대 4시간 미만을 충전 또는 방전한다.

HVDC 용량 및 운용 조건

- H C ≤ h v d c t 1,1 ≤ H C - H C ≤ h v d c t 1,2 ≤ H C ∑ t t = t + 1 t + m i n 5, T e n d - t - 1 1 - h t 3 ≥ h t 5 - h t + 1 5 × m i n (6, T e n d - t) ∑ t t = t + 1 t + m i n 5, T e n d - t - 1 1 - h t 5 ≥ h t 3 - h t + 1 3 × m i n (6, T e n d - t) ∑ t t = t + 1 t + m i n (5, (T e n d - t - 1) 1 - h t 6 ≥ h t 4 - h t + 1 4 × m i n (6, T e n d - t) h t 4 = 1 - h t 3 - h t 5, h t 3 = 1 - h t 4 - h t 6 h t 1 + h t 3 + h t 5 = 1, h t 2 + h t 4 + h t 6 = 1 ∑ t ∈ T h t 3 + h t 5 ≥ ∑ t ∈ T h t 1 ∑ t ∈ T h t 4 + h t 6 ≥ ∑ t ∈ T h t 2, ∀ t ∈ T

(11)

HVDC의 운영 방식은 곽은섭･민재현･정호철･문채주(2021)의 연구에서의 HVDC 운전 방식을 참고하였으며, 식 (11)은 HVDC#1의 운전 방식을 의미하며, 정송일 경우 두 개의 pole이 같이 전력을 공급받을 수 있지만 역송일 경우 1개의 pole로만 전력을 역송하도록 운행된다. 정송에서 역송 또는 역송에서 정송으로 운영이 바뀔 때 최소 6시간의 운전정지시간이 필요하므로 최소 6시간의 정지 후에 다시 운행을 진행한다.

- H C ≤ h v d c t 2,1 ≤ H C - H C ≤ h v d c t 2,2 ≤ H C ∑ t t = t + 1 t + m i n 5, T e n d - t - 1 1 - h t 7 ≥ h t 8 - h t + 1 8 × m i n 6, T e n d - t ∑ t t = t + 1 t + m i n 5, T e n d - t - 1 1 - h t 8 ≥ h t 7 - h t + 1 7 × m i n 6, T e n d - t h t 7 + h t 8 + h t 9 = 1 ∑ t ∈ T h t 7 + h t 8 ≥ ∑ t ∈ T h t 9, ∀ t ∈ T

(12)

식 (12)는 HVDC#2의 운전 방식을 의미하며, 최소 송전량을 기준으로 하여 두 개의 pole이 함께 정송을 하거나 역송을 하도록 운행된다. HVDC#1과 마찬가지로 정송에서 역송 또는 역송에서 정송으로 운영이 바뀔 때 최소 6시간의 운전정지시간이 필요하므로 최소 6시간의 정지 후에 다시 운행을 진행한다.

- H C ≤ h v d c t 3,1 ≤ H C

(13)

식 (13)은 HVDC#3의 운전 방식을 의미하며, HVDC#3의 경우 정송과 역송 변환에 필요한 정지시간이 짧기 때문에 1개의 pole이 정송과 역송 변환을 자유롭게 하도록 운행된다.

h v d c t = h v d c t 1,1 + h v d c t 1,2 + h v d c t 2,1 + h v d c t 2,2 + h v d c t 3,1, ∀ t ∈ T

(14)

출력제어율 조건

∑ t ∈ T S P t + W P t - v r t / ∑ t ∈ T S P t + W P t ≤ C u r, ∀ t ∈ T

(15)

식 (15) 은 출력제어율은 발전하였으나 사용하지 못한 신재생에너지 양과 총발전한 신재생에너지 양의 비율을 의미한다. 시나리오에 따라 목표 출력제어율을 설정해 주었으며, 설정한 목표 출력제어율에 대한 조건식이다.

수요 충족 조건

∑ g ∈ G p g, t 2 + e × e s s 1 t + e s s 2 t 1 + e s s 2 t 2 + h v d c t + v r t = L o a d t, ∀ t ∈ T, ∀ g ∈ G

(16)

식 (16)은 시간별 부하 기동일때 발전기의 전력 생산량, ESS의 충, 방전에 다른 전력량, HVDC의 정, 역송량과 재생에너지 발전량의 합으로 시간별 전력 수급 균형을 이루어야 하는 제약을 의미한다.

Ⅳ. ESS 용량 결정 경제급전 모델 시뮬레이션

1. 기본 전제

2030년 제주 전력 계통에서 에너지저장시스템(ESS)을 도입하지 않는 현행 유지 시나리오와 출력제어율을 3% 이하 및 5% 이하로 각각 제한하는 시나리오를 구성하였다. 구체적으로, 재생에너지 발전원의 변동성에 대응하는 단주기 ESS와 출력제어율 완화를 위한 장주기 ESS를 함께 고려하였으며, 제10차 전력수급기본계획에서 제시된 발전설비 계획과 더불어 이미 설치된 HVDC #1, #2 및 2023년 준공 예정인 HVDC #3의 운전 방식을 적용하였다. 또한, 계획상 신규 발전기는 기존 발전기 중 설비용량과 발전 방식이 가장 유사한 사례로 가정하여 시뮬레이션에서 사용하였다.

2. 입력 자료

1) 발전기 기술 입력 자료

시뮬레이션에 적용한 발전기의 기술 입력자료는 김용건 등(2019), 전력통계정보시스템(2021) 및 정보공개 청구를 통해 얻은 데이터를 재구성하여 사용하였다. 발전원별 최대 증감발량, 최소 정지시간 및 운전 시간, 열효율 및 최소 발전량 비율에 대해선 평균값으로 <표 2, 3, 4>에 제시하였다. 발전기의 최대 발전 용량은 설비용량으로 대체하였으며 <표 1>과 같다.

<표 1>

제주지역 발전기 설비용량 데이터

<표 2>

발전원별 평균 최대 증감발량

<표 3>

발전원별 평균 최소 정지시간 및 운전시간

<표 4>

발전원별 평균 열효율

2) 발전기 비용 입력자료

발전기 비용 입력자료는 김용건 등(2019), 전력통계시스템(2021)³⁾ 및 정보공개 청구 데이터를 참조하였다. 발전원별 열량 단가는 10년간의 평균을 사용하였으며, 기동 비용은 재구성하여 평균값으로 나타내었다.

발전원별 평균 최소 발전량 비율

발전원별 열량 단가 및 운전 유지비용

발전원별 평균 기동비용

발전원별 온실가스 배출 계수

3) 전력 수요 입력 자료

제10차 전력수급기본계획에 따르면, 2021년(실적 기준) 최대 전력량은 1,036MW이며 2030년에는 약 1,572MW로 증가할 것으로 예측된다(약 1.5174배 상승). 본 연구에서는 한국 전력거래소(2021)⁴⁾를 참고하여 2021년과 2030년의 최대전력 상승률을 고려하였고, 이를 통해 추정한 2030년 제주도의 시간대별 전력 수요를 시뮬레이션에 반영하였다. <그림 1>에는 한 달간의 시간당 전력 수요 예측치를 예시로 제시하였다.

<그림 1>

제주지역 시간당 전력 수요량자료: 산업통상자원부(2023)와 한국전력거래소, 2021, https://www.kpx.or.kr.

4) 재생에너지 설비 및 ESS 관련자료

재생에너지 설비용량은 제10차 전력수급기본계획을 기반으로 설정하였다. 단주기 ESS의 경우 리튬이온배터리를 사용하며, 산업통상자원부(2018),⁵⁾송홍석(2019), 문찬호･권보성･우수화･배동진･송경빈(2020)을 참조하여 기술 특성과 설치 비용을 <표 10>에 정리하였다. 장주기 ESS는 바나듐 레독스 플로우 배터리를 사용하며, United States Department of Energy(2022) 및 United States Department of Energy(2019)를 참고하여 <표 11>에 기술 특성과 설치비용을 제시하였다.

<표 9>

2030 제주 재생에너지 설비용량

<표 10>

단주기 ESS 입력자료

<표 11>

장주기 ESS 입력자료

5) HVDC 입력 자료

제주와 육지를 연결하는 HVDC 설비(완공 및 준공 예정 포함)에 대한 기술 파라미터는 곽은섭 등(2021)과 최지웅･이호준･장정수･윤민한(2023)을 참조하였으며, 운영 유지비용･전송 비용은 DeSantis et al.(2021)과 Acaroğlu & MárquezA(2022)를 기반으로 <표 12, 13, 14>과 같이 정리하였다.

<표 12>

제주-육지 HVDC 입력자료

<표 13>

제주-육지 HVDC 파라미터

<표 14>

HVDC 운영 유지비용 및 전송 비용

3. ESS 최적 용량 결정 시나리오

곽은섭 등(2021)을 참고하여 HVDC#1의 경우 일반제어 모드 및 reverse mode 운전을 하며 HVDC#2는 일반제어 모드 운전한다. 또한, HVDC의 최소 송전용량 제약을 고려하였다. ESS를 도입하지 않고 기존 전력 설비만을 사용하는 현행 유지 시나리오와 목표 출력제어율인 3% 이하, 5% 이하를 충족하는 시나리오를 구성하여 <표 15>와 같이 구성하였으며 장단주기 ESS의 최적 용량을 도출하였으며 현행을 유지한 경우와 ESS를 도입하였을 때 기존 전력 설비 및 재생에너지의 이용률 변화를 비교하고 발전기의 출력패턴을 분석하였다.

<표 15>

ESS 도입 여부에 따른 시나리오

4. 시뮬레이션 결과

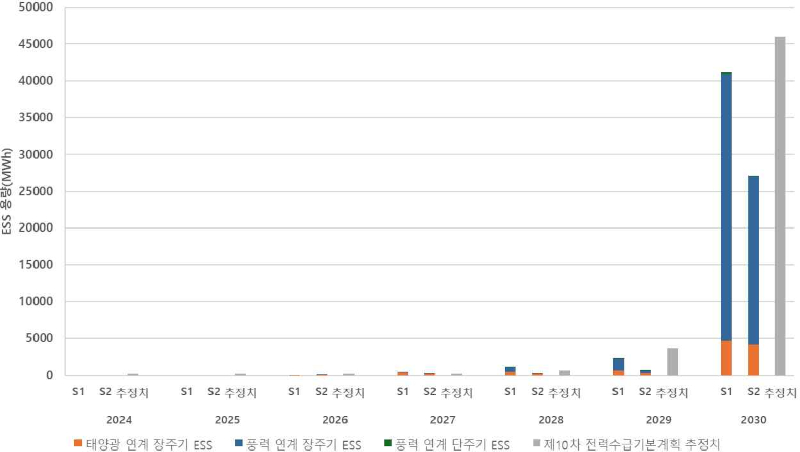
혼합 정수 선형계획법(MILP)으로 구성된 최적화 문제를 풀기 위해 CPLEX Solver를 사용하였다. 시뮬레이션 결과를 요약한 <표 16>은 HVDC 역송 조합에 따른 시나리오별 ESS 최적 용량을 보여주며, <그림 2>는 연도별 시나리오에 따른 누적 ESS 용량 추이와 더불어, 산업통상자원부(2023)에서 제시한 제10차 전력수급기본계획의 ESS 필요량 추정치를 함께 비교하였다.

<표 16>

시나리오별 최적 ESS 용량

<그림 2>

시나리오별 및 제10차 전력수급기본계획 총 ESS 용량 추이

시나리오별 및 제10차 전력수급기본계획 모두 재생에너지 설비용량이 확대됨에 따라 ESS 필요 용량이 증가함을 보여주며, 특히 2030년에 ESS 용량이 급격히 증가하는 양상이 두드러진다. 이는 같은 해 태양광 95MW, 풍력 834MW 등 총 929MW의 재생에너지가 추가로 보급될 예정이어서,⁶⁾ 계획 연도 중 가장 큰 규모의 재생에너지 설비 확장이 이뤄지기 때문이다. 하지만 제10차 전력수급기본계획의 ESS 필요량 추정치와 비교해 보면, 본 논문의 시뮬레이션에서 도출된 총 ESS 용량이 다소 낮은 값을 나타낸다. 이는 계획안에서는 장주기 ESS만을 고려하는 반면, 본 연구에서는 출력제어율 완화를 위한 장주기 ESS와 변동성 대응을 위한 단주기 ESS를 모두 포함했기 때문으로 해석된다.

또한, ESS가 전혀 도입되지 않는 현행 유지 시나리오(시나리오3)의 경우 2029년부터 출력제어율이 약 8%로 급격히 증가한다. 이는 재생에너지 설비가 늘어도 해당 시점까지는 전력 수요와 HVDC 역송만으로 발전량을 수용할 수 있지만, 2029년 이후에는 급증하는 재생에너지 출력을 더 이상 감당하기 어려워지는 것을 의미한다. 이에 반해 ESS를 도입한 시나리오에서는 2027년까지 풍력 연계 ESS 필요량이 적다가, 2029년부터 전년 대비 큰 폭으로 증가하며, 특히 목표 출력제어율을 3% 이하로 설정한 시나리오1이 시나리오2(5% 이하)보다 더 많은 ESS 용량 도입이 요구된다.

재생에너지 확대에 따라 기존 발전설비 이용률도 변화한다. 2021년 대비 2030년의 경우, 현행 유지 시나리오(시나리오3)에서는 재생에너지 보급이 많이 늘어나면서 기존 발전설비 이용률이 34.65%에서 30.11%로 감소하였고, ESS를 도입한 시나리오1(22.96%), 시나리오2(23.86%)에서는 이보다 더 큰 폭으로 감소한다. 이는 ESS 도입으로 더 많은 재생에너지를 흡수할 수 있기 때문에, 기존 발전기 이용률이 상대적으로 줄어드는 결과다. 동시에, 출력제어율이 현행 유지 시나리오에서는 2029년 약 8%, 2030년 약 20%까지 치솟음에 따라 태양광과 풍력 이용률이 각각 10.33%, 17.21%에 머무는 반면, 시나리오1에서는 13.56%(태양광), 20.3%(풍력)로, 시나리오2에서는 13.51%(태양광), 19.75%(풍력)로 높게 나타난다.

<그림 2>

2030년 10월 1일 시나리오1 일일 출력패턴

<그림 3>

2030년 10월 1일 시나리오2 일일 출력패턴

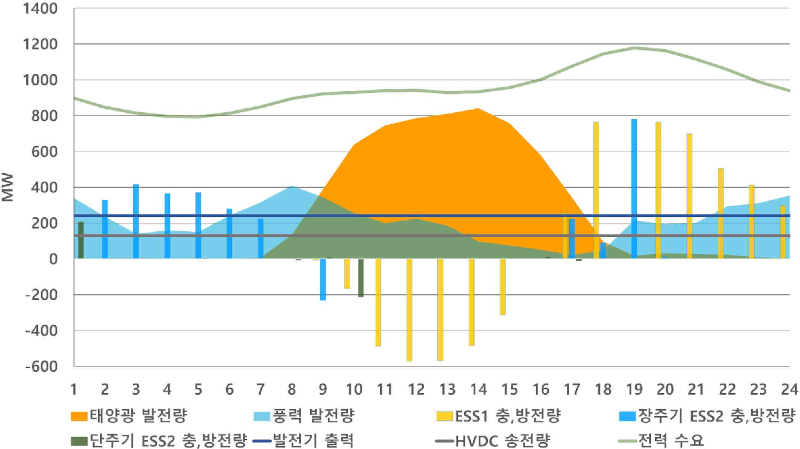
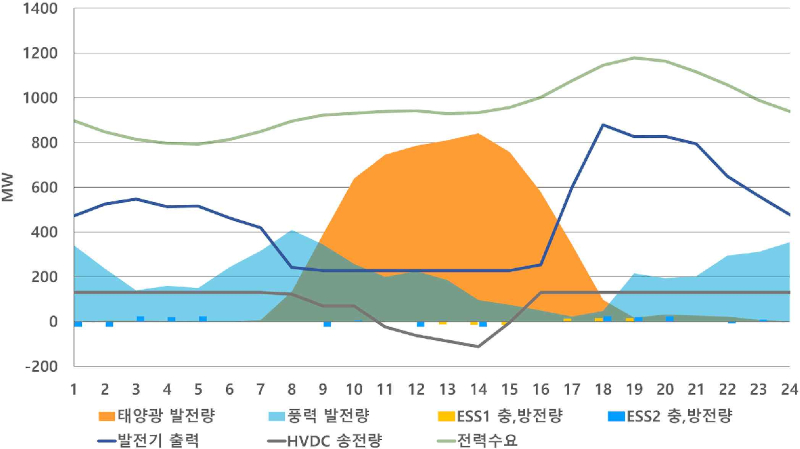
시나리오3(현행 유지)의 출력패턴(<그림 4>)을 살펴보면, 재생에너지 발전량이 증가하는 낮 시간대 순 부하량(net load)이 급격히 감소하면서 이른바 ‘duck curve’ 현상이 나타난다. 이에 따라 7시와 8시, 21시와 22시, 23시와 24시, 16시와 18시 사이 등의 시간대에 각각 100~300MW 안팎의 급격한 Ramp up/down이 발생하며, 발전기에 큰 부담이 된다. 반면, ESS를 도입하는 시나리오1, 2에서는 재생에너지를 배터리에 저장하여 발전기의 급격한 출력 감소를 방지하고, 전력 수요가 증가하거나 감소하는 시간대에 ESS를 활용해 대응함으로써 발전기 부담을 완화할 수 있다. 특히 시나리오1이 시나리오2보다 ESS 용량이 커, 발전기에 더욱 안정적인 운전 여건을 제공하지만, 그만큼 ESS 도입 비용이나 기존 설비의 낮은 이용률도 고려해야 한다.

<그림 4>

2030년 10월 1일 시나리오3 일일 출력패턴

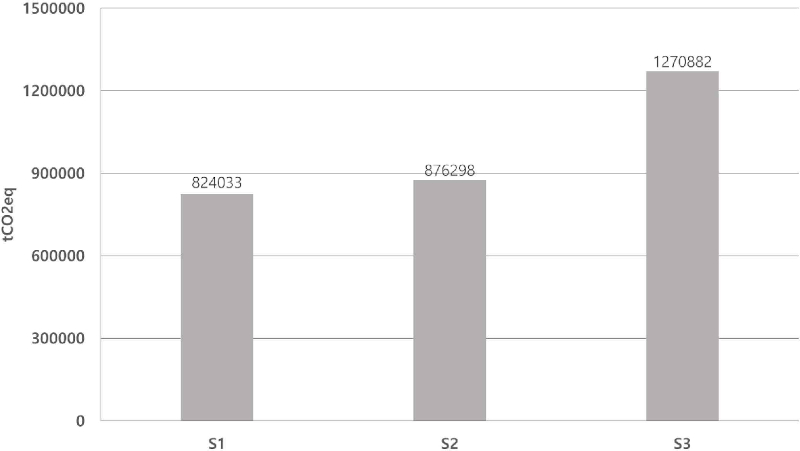
한편, 제주특별자치도(2022)에 따르면 2018년 발전 부문 탄소 배출량은 약 1,066천 톤 CO2eq이다. <그림 5>에서 시나리오3은 약 20%라는 출력제어율과 동시에 늘어난 전력 수요로 인해, 2018년에 비해 오히려 더 많은 탄소가 배출된다. 반면 시나리오1과 시나리오2는 ESS 도입으로 재생에너지 활용도가 높아져 2018년 대비 탄소 배출량이 감소하며, 특히 시나리오1은 시나리오2보다 약 5% 이상의 추가 감축 효과가 있다. 제주가 2030년까지 2018년 대비 약 40% 이상의 온실가스를 감축해야 한다는 점을 고려하면, 시나리오1이 더욱 바람직한 대안이라는 점을 확인할 수 있다.

<그림 5>

시나리오별 2030년 발전 부문 탄소 배출량

4. 시나리오별 비용분석

서술한 바와 같이 본 연구에서는 목적함수에 포함된 전력 계통 운영 전반의 비용을 고려하였다. 구체적으로 발전기 발전 비용, HVDC 송전･정송･유지 보수 비용, ESS 설치･유지 보수 비용, 그리고 탄소배출권 가격(8년 평균치 적용)에 기반한 탄소 배출 비용을 합산하고, ESS 설비의 잔존 가치 또한 반영하였다. 사회적 할인율은 4.5%로 가정하였으며, 순현재가치(Net Present Value, NPV) 방식으로 비용을 산출하였다.

<표 17>의 시나리오1과 시나리오3을 살펴보면 ESS 설비비용이 상당히 크지만 발전 비용의 차이는 1,089억 원, 탄소배출 비용의 차이는 59억 원으로 나타난다. 특히 2030년의 발전 비용 차이와 탄소배출 비용 차이는 각각 795억 원, 53억 원으로, 2030년 한 해만 놓고 보면 ESS를 통한 발전 비용 및 탄소배출 비용 절감 효과가 상대적으로 작었다. 이는 ESS 최적 용량의 약 95%가 2030년에 도입되면서 해당 시점 이전까지는 ESS로 인한 절감 효과가 제한적이었기 때문으로 해석된다.

<표 17>

2030년까지 시나리오별 비용분석[억원]

이러한 점을 반영하여, 재생에너지 설비용량 및 ESS 용량을 2030년 결괏값으로 가정하되, 계획 연도를 제10차 전력수급기본계획의 기간(2036년)까지 확장하여 비용분석을 수행한 결과는 <표 18>과 같다.

<표 18>

2036년까지 시나리오별 비용분석[억원]

2030년까지의 결과(<표 17>)와 비교해 <표 18>의 결과를 보면, 목표 출력제어율을 설정한 시나리오(S1, S2)와 현행 유지 시나리오(S3) 간 총비용 격차가 감소했음을 확인할 수 있다. 구체적으로 시나리오1과 S3를 비교할 때 약 30%, 시나리오2와 S3를 비교할 때 약 43% 정도 격차가 줄어든다. 이는 시간이 지날수록 ESS 도입을 통해 발전 비용, 탄소배출 비용, HVDC 운용 비용을 절감할 수 있어, 결과적으로 시스템 총비용 차이가 완화되는 것을 의미한다.

한편, 2030년까지의 비용분석에서 시나리오1과 시나리오2를 비교해 보면 발전 비용 차이는 353억 원, 탄소배출 비용 차이는 9억 원으로, ESS 설비비용 차이(6,217억 원)에 비해 상대적으로 적었다. 2036년까지 확장해서 보아도 발전 비용 차이는 755억 원, 탄소배출 비용 차이는 46억 원으로, 여전히 ESS 설비비용 차이 대비 작게 나타난다.

결국 더 낮은 목표 출력제어율(예: 시나리오1)을 달성하기 위해 추가적인 ESS를 도입할수록 재생에너지 이용률 상승과 발전기 출력 변동 폭･횟수 감소, 탄소배출 저감 같은 편익이 커지지만, 그에 상응하는 투자 비용도 많이 증가함을 확인할 수 있다. 특히 2030년까지 3%와 5% 목표 출력제어율 달성을 위해서는 약 5,800억 원 이상의 추가 비용이 발생하는 것으로 나타나, 재생에너지 이용률･기존 발전설비 이용률 간의 균형을 어떻게 맞출지 면밀한 검토가 필요하다는 점을 시사한다.

Ⅴ. 결론

본 논문에서는 제주 CFI 2030을 위해 재생에너지 설비의 증가에 따른 출력제어율의 증가를 방지하기 위해 장주기, 단주기 ESS 설비의 보급 증가를 적용하였으며, HVDC 운전 방식을 적용한 경제급전을 통해 현행 유지할 경우와 목표 출력제어율에 따른 ESS의 최적 용량을 산정하였고 비용분석을 수행하였다.

사례 분석 결과, 목표 출력제어율에 따른 시나리오별로 태양광 연계 ESS, 풍력 연계 단주기 ESS, 풍력 연계 장주기 ESS의 설비용량과 총용량의 최적 용량으로 목표 출력제어율 3%의 경우 태양광 연계 ESS 763MW/4,629MWh, 풍력 연계 단주기 ESS 212MW/265MWh, 풍력 연계 장주기 ESS 1,422MW/ 36,318MWh, 목표 출력제어율 5%의 경우 태양광 연계 ESS 710MW/ 4,120MWh, 풍력 연계 단주기 ESS 21MW/26MWh, 풍력 연계 장주기 ESS 1,162MW/22,827MWh로 검토된다. 현행 유지와 비교한 설비 이용률 분석에서 볼 수 있듯이 ESS를 도입하였을 때 재생에너지의 이용률이 상승한다. 2030년 10월 1일 일일 출력 패턴에서도 발전기의 출력 변동 폭과 Ramp up/down 횟수가 줄어들었으며 출력제어율 또한 현행 유지에서는 약 20%이었던 것이 ESS를 추가 도입 시 3% 및 5% 이하로 낮아지는 것으로 나타났다. 탄소 배출량 또한 약 400천 톤 CO2eq 이상 줄어들어 탄소 중립이라는 목표를 위해 ESS 보급이 필수적임을 보여준다. 또한, ESS의 보급이 더 많을수록 발전기의 출력 변동 폭 및 Ramp up/down 횟수가 더 줄어들었으며, 재생에너지 이용률은 더 증가하는 것을 보여준다. 하지만, 비용분석 결과 시나리오2의 목표 출력제어율보다 더 낮은 목표 출력제어율을 달성하기 위해 ESS를 더 보급한 시나리오1의 경우 ESS 설비 투자 비용이 매우 큰 것으로 나타난다, 시나리오2 대비 시나리오1의 경우 2018년 대비 온실가스 배출 감축량 효과가 5% 더 높았기 때문에 CFI 2030 목표 온실가스 배출 감축을 위해서라도 시나리오1의 상황이 더 필요한 것을 보여준다. 따라서, 3% 목표 출력제어율을 위한 ESS 도입 시 ESS 설비 투자 비용에 대한 정책적인 방안을 마련해야 할 것으로 판단된다.

Acknowledgments

This work was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2023S1A5A2A21085534). This work was supported by the Korea Institute of Energy Technology Evaluation and Planning(KETEP) and the Ministry of Trade, Industry & Energy(MOTIE) of the Republic of Korea (20224000000090).

Notes

1) 산업통상자원부(2023)을 참조.

2) 제주일보, 2023.4.18., “제주~완도 잇는 해저케이블 연말까지 준공,” https://www.jejunews.com/news/articleView.html?idxno=2202214

3) 전력통계정보시스템, 2021, https://epsis.kpx.or.kr.

4) 한국전력거래소, 2021, https://www.kpx.or.kr.

5) 산업통상자원부, 2018, https://www.motie.go.kr.

6) 산업통상자원부(2023)를 참조.

References

김병오･곽규형･김태현･신한솔･김욱, 2021, “가격결정발전계획을 고려한 대용량 ESS 최적용량 산정, 『전기학회논문지』, 45(3), pp.259-277.
김용건･구윤모･김동우･이원종･양유경, 2019, “혼합정수계획법을 이용한 발전부문 온실가스 감축 잠재력평가”, 『기후환경정책연구』, 2019권, pp.1-96.
김자현･한가희･문희승, 2022, “2030 탄소 없는 섬 제주도, 출력제한 없는 섬에서부터: 재생에너지 출력제한 문제 해결방안의 비용분석”, 서울: 기후솔루션.
김창수･최상봉, 2020, “PV 연계형 ESS의 설치 규모에 따른 수익영향”, 『Current Photovoltaic Research』, 8(3), pp.86-93.
곽은섭･민재현･정호철･문채주, 2021, “제주 지역 재생에너지 수용을 위한 HVDC 및 BESS 활용에 대한 연구”, 『한국전자통신학회 논문지』, 16(6), pp.1339- 1348.
문찬호･권보성･우수화･배동진･송경빈, 2020, “SMP와 REC가격 변동 시나리오에 따른 사업자 관점에서 태양광 발전 사업의 경제성평가 및 민감도 분석”, 조명･전기설비학회논문지』, 34(10), pp.36-44.
백민규･박종배･손성웅･신하상･박용기, 2018, “태양광 연계형 배터리 에너지 저장장치의 최적 용량 산정”, 『전기학회논문지』, 67(1), pp.38-45.
산업통상자원부, 2023, 『제10차 전력수급기본계획』, 세종: 산업통상자원부.
송홍석, 2019, “신재생에너지 및 ESS용 PCS의 최신 동향”, 『KIPE Magazine』, 24(5), pp.58-63.
이용봉･김정호, 2015, “태양광/풍력 연계 기반의 ESS 경제성 분석”, 『에너지공학』, 24(3), pp.74-81.
제주일보, 2023.4.18., “제주~완도 잇는 해저케이블 연말까지 준공,” https://www.jejunews.com/news/articleView.html?idxno=2202214, .
제주특별자치도, 2022, 『2050 탄소중립 위한 제주특별자치도 기후변화 대응 계획』, 제주: 제주특별자치도.
최윤석･나승유, 2018, “PV-BESS 시스템의 적정 PCS, 배터리용량 산정에 따른 최적 운영에 관한 연구”, 『전기학회논문지』, 67(9), pp.1174-1180.
최지웅･이호준･장정수･윤민한, 2023, “HVDC 운영 전략에 따른 제주 전력 계통의 출력제어 및 운영비용 분석”, 『전기학회논문지』, 72(6), pp.701-708.
Acaroğlu, H. and Márquez, F. P. G., 2022, “A life-cycle cost analysis of High Voltage Direct Current utilization for solar energy systems: The case study in Turkey”, Journal of Cleaner Production, 360, 132128. [https://doi.org/10.1016/j.jclepro.2022.132128]
Baldick, R., 1995, “The Generalized Unit Commitment Problem”, IEEE Transactions on Power Systems, 10(1), pp.465-475. [https://doi.org/10.1109/59.373972]
DeSantis, D., James, B. D., Houchins, C., Saur, G. and Lyubovsky, M., 2021, “Cost of long-distance energy transmission by different carriers”, IScience, 24(12). [https://doi.org/10.1016/j.isci.2021.103495]
Mahmood, M. A. and Al-Anbarri, K. A., 2022, “An Optimal Solution to The Unit Commitment Problem for A Hybrid Power System”, 2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), pp.1-8. [https://doi.org/10.1109/HORA55278.2022.9799985]
Michi, L., et al., 2019, “New HVDC technology in Pan-European power system planning.“, 2019 AEIT HVDC International Conference (AEIT HVDC), pp. 1-6 [https://doi.org/10.1109/AEIT-HVDC.2019.8740544]
Vatsal, D., Sharma, V., & Sharma, K. C., 2023, “Fast frequency response constrained unit commitment for low inertia grids.“, 2023 International Conference on Recent Advances in Electrical, Electronics & Digital Healthcare Technologies (REEDCON), pp. 734-739 [https://doi.org/10.1109/REEDCON57544.2023.10150820]
United Sates Department of Energy, 2022, “ESGC Cost Performance Report”.
United Sates Department of Energy, 2019, “Storage Cost and Performance Characterization Report”.
산업통상자원부, 2018, https://www.motie.go.kr, .
전력통계정보시스템, 2021, https://epsis.kpx.or.kr, .
한국석유관리원, 2023, https://www.kpetro.or.kr, .
한국전력거래소, 2021, https://www.kpx.or.kr, .

Appendix

<부록 1> 기호 및 약어 정의

1) 집합


y∈Y :	설비 계획년도 인덱스
t, tt∈T :	전체 시간 인덱스
g∈G :	발전기 인덱스
must∈G :	필수 운전 발전기
c∈ch :	ESS 충전 시간 인덱스
d∈dc :	ESS 방전 시간 인덱스
i∈I :	HVDC 인덱스
j∈J :	HVDC pole 인덱스

2) 파라미터


dr :	사회적 할인율(4.5%)
SMP :	10년 평균 SMP
FC_g :	열량 단가(원/Gcal)
H₁, H₀ :	발전기 열효율 함수 1차 계수 및 상수
OM_g :	발전기 운영비용
SC_g :	발전기 기동 비용
Load_t :	전력 수요량
MU_t :	발전기 최소 가동시간
MD_t :	발전기 최소 정지시간
SP_t :	시간별 태양광에너지 총 발전량
WP_t :	시간별 풍력에너지 총 발전량
$P g m i n$ :	발전기 최소발전량
$P g m a x$ :	발전기 최대발전량
FM_t :	고정된 필수 가동 발전기 수
RU_g :	최대 증발량
RD_g :	최대 감발량
SRU_g :	기동시 증발량
WRD_g :	정지시 감발량
e :	장주기, 단주기 ESS 충,방전 효율
HC :	시나리오별 HVDC 용량
HP :	HVDC 운영비용
ElC1 :	장주기 ESS 설치비용
ElC2 :	단주기 ESS 설치비용
PlC1 :	장주기 PCS 설치비용
PlC2 :	단주기 PCS 설치비용
EP1 :	장주기 ESS 유지보수비용
EP2 :	단주기 ESS 유지보수비용
life^long :	장주기 ESS 설계수명
life^short :	단주기 ESS 설계수명
CC :	탄소배출비용
C_g :	발전기 발전원별 탄소배출계수
Cur :	시나리오별 목표 출력제어율

3) 변수


p_g,t :	발전기 발전량
$p g, t 1$ :	무부하기동 발전량
$p g, t 2$ :	부하기동 발전량
p_g,t :	기동 여부(이진변수)
$u g, t 1$ :	무부하기동 여부(이진변수)
$u g, t 2$ :	부하가동 여부(이진변수)
v_g,t :	기동 여부(이진변수)
w_g,t :	정지 여부(이진변수)
ess1_t :	태양광에너지 연계 에너지저장장치 충, 방전량
$e s s 2 t 1$ :	풍력에너지 연계 장주기 에너지저장장치 충, 방전량
$p 1 t e s s 21$ :	풍력에너지 연계 장주기 에너지저장장치 충전량
$p 2 t e s s 21$ :	풍력에너지 연계 장주기 에너지저장장치 방전량
$u 1 t e s s 21$ :	풍력에너지 연계 장주기 에너지저장장치 충전여부(이진변수)
$u 2 t e s s 21$ :	풍력에너지 연계 장주기 에너지저장장치 방전여부(이진변수)
$p 1 t e s s 22$ :	풍력에너지 연계 단주기 에너지저장장치 충전량
$p 2 t e s s 22$ :	풍력에너지 연계 단주기 에너지저장장치 방전량
$u 1 t e s s 22$ :	풍력에너지 연계 단주기 에너지저장장치 충전여부(이진변수)
$u 2 t e s s 22$ :	풍력에너지 연계 단주기 에너지저장장치 방전여부(이진변수)
hvdc_t :	초고압 직류 역송 및 정송량
$h v d c t i, j$ :	i번째 HVDC의 j번째 pole의 역송 및 정송량
$h t 1, h t 2$ :	첫 번째 HVDC 각 pole의 정지상태 여부(이진변수)
$h t 3, h t 4$ :	첫 번째 HVDC 각 pole의 역송상태 여부(이진변수)
$h t 5, h t 6$ :	첫 번째 HVDC 각 pole의 정송상태 여부(이진변수)
$h t 7$ :	두 번째 HVDC 정지상태 여부(이진변수)
$h t 8$ :	두 번째 HVDC 역송상태 여부(이진변수)
$h t 9$ :	두 번째 HVDC 정송상태 여부(이진변수)
vr_t :	재생에너지 총 발전량
vs_t :	태양광에너지 발전량
vw_t :	풍력에너지 발전량
el1_t :	태양광에너지 연계 장주기 에너지저장장치 충전상태량
$e l 2 t 1$ :	풍력에너지 연계 장주기 에너지저장장치 충전상태량
$e l 2 t 2$ :	풍력에너지 연계 단주기 에너지저장장치 충전상태량
e1c_t :	태양광에너지 연계 에너지저장장치 총용량
$e 2 c t 1$ :	풍력에너지 연계 장주기 에너지저장장치 총용량
$e 2 c t 2$ :	풍력에너지 연계 단주기 에너지저장장치 총용량
p1c_t :	태양광에너지 연계 에너지저장장치 설비용량
$p 2 c t 1$ :	풍력에너지 연계 장주기 에너지저장장치 설비용량
$p 2 c t 2$ :	풍력에너지 연계 단주기 에너지저장장치 설비용량

<부록 2> 발전기, 신재생에너지 제약조건

무부하기동 및 부하기동에 따른 발전량 및 작동상태 조건

$p g, t = p g, t 1 + p g, t 2 u g, t = u g, t 1 + u g, t 2, u g, t 1 + u g, t 2 ≤ 1, ∀ t, ∀ g$

발전기 상태 조건

$u g, t + 1 2 - u g, t 2 = v g, t - w g, t v g, t + w g, t ≤ 1, ∀ t, ∀ g$

발전기 최소 운전 시간 조건

$∑ t t = t + 1 t + m i n M U g - 1, T e n d - t - 1 + 1 u g, t 2 ≥ u g . t + 1 2 - u g, t 2 × m i n M U g, T - t, ∀ t, ∀ g$

발전기 최소 정지시간 조건

$∑ t t = t + 1 t + m i n M D g - 1, T e n d - t - 1 1 - u g, t 2 ≥ u g . t 2 - u g, t + 1 2 × m i n M D g, T - t, ∀ t, ∀ g$

발전기 최대 증감발량 조건

$p g, t + 1 - p g, t ≤ R U g × 1 - v g, t + S R U g × v g, t p g, t - p g, t + 1 ≤ R D g × 1 - w g, t + W R D g × w g, t, ∀ t, ∀ g$

필수 가동 발전기 조건

$∑ t ∈ T ∑ g ∈ m u s t u g, t 2 = F M t, ∀ t, ∀ g$

발전량 조건

$p g, t 1 ≤ u g, t 1 × P g m i n p g, t 2 ≥ u g, t 2 × P g m i n p g, t 2 ≤ u g, t 2 × P g m a x, ∀ t, ∀ g$

태양광,풍력에너지 발전량 조건

$v r t = v s t + v w t v s t ≤ S P t v w t ≤ W P t, ∀ t ∈ T$

이성준: 부산대학교 산업공학과 학사 수료 후, 현재 지능･물류･빅데이터연구소의 연구보조원으로 발전 최적화 연구를 수행하고 있다. 주요 관심 분야는 환경급전･발전 최적화 등이 있다(leesjun2018@naver.com).

이주은: 부산대학교 산업공학과 석사과정에 재학 중이다. 주요 관심 분야는 경제급전･신재생에너지･탄소배출이 있다. 현재 유전알고리즘을 활용한 연구를 진행 중이다(aguero0619@pusan.ac.kr).

박원빈: 부산대학교 산업공학과 석사과정에 재학 중이다. 주요 관심 분야는 기후변화･환경규제를 고려한 발전 최적화 등이 있다(park1bin@pusan.ac.kr).

윤설아: 부산대학교 산업공학과 학사학위를 취득하였다. 주요 관심 분야는 빅데이터, AI, 머신러닝 등이다(seola8268@naver.com).

김주연: 부산대학교 산업공학과에서 학사학위를 취득하고 한화오션 기계 의장팀에서 재직 중이다(juyeons1119@naver.com).

김도원: 부산대학교 산업공학과에서 학사를 취득하였고 KAIST에서 산업및시스템 공학을 전공하였으며 공학 석사와 박사를 취득하였다. 현재 기후-에너지 모델링이 주요 연구분야이며 추계적 최적화 및 시뮬레이션을 주요 방법론으로 활용하고 있다(dowon.kim@pusan.ac.kr).

발전기명	설비용량[MW]	비고
자료: 전력통계정보시스템, 2021, https://epsis.kpx.or.kr와 정보공개 청구
남제주복합	146.24
남제주#1	100	필수 가동 발전기
남제주#2	100
한림복합	105	필수 가동 발전기
제주화력#2	75	필수 가동 발전기
제주화력#3	75	필수 가동 발전기
제주LNG복합CC1	114.36
제주LNG복합CC2	114.36
제주내연#1	40	필수 가동 발전기
제주내연#2	40	필수 가동 발전기

구분	유류[시간]	바이오중유[시간]	복합화력[시간]
최소 운전시간	4	7.2	2.6
최소 정지시간	3.6	7.8	2.4

구분	유류	바이오중유	복합화력
1차 계수	0.862931	1.79447	1.66554
상수 계수	42.566805	31.584268	35.95

구분	유류	바이오중유	복합화력
자료: 김용건 등(2019)과 전력통계정보시스템, 2021, https://epsis.kpx.or.kr
열량 단가[원/Gcal]	78166.44	78166.44	64971.33
운전 유지비용[원/MWh]	1490	1490	2730

구분	유류 [톤CO₂eq/MWh]	바이오중유 [톤CO₂eq/MWh]	복합화력 [톤CO₂eq/MWh]
자료: 김용건 등(2019)과 한국석유관리원, 2023, https://www.kpetro.or.kr.
온실가스 배출계수	0.6271	0.094	0.4139

ESS 입력자료
자료: 문찬호 등(2020), 산업통상자원부, 2018, https://www.motie.go.kr.와 송홍석(2019)
충/방전 효율	충전[95%] / 방전[95%]
SOC 범위	정격용량의 10[%]~90[%]
설계수명	10년
초기투자비용(PCS등 포함)	540000[천원/MWh]
ESS 연간 운영 유지비용 (설치 비용의 3%)	16200[천원/MWh]

ESS 입력자료
자료: United States Department of Energy(2022)와 United States Department of Energy(2019)
충/방전 효율	충전[75%] / 방전[75%]
SOC 범위	정격용량의 10[%]~90[%]
설계수명	20년
ESS 설치비용	386[$/kWh]
PCS 설치비용	73[$/kW]
ESS 연간 운영 유지비용	10[$/kW]

연계선	HVDC#1	HVDC#2	HVDC#3
자료: 곽은섭 등(2021)
구간	제주-해남	서제주-진도	동제주-완도
변환설비	전류형	전류형	전압형
설비용량	150MW × 2P, DC ± 180kV	200MW × 2P, DC ± 250kV	200MW × 2P, DC ± 150kV

구분	HVDC#1	HVDC#2	HVDC#3
최대 송전(1 pole당)	75MW	125MW	200MW
최소 송전(1 pole당)	15MW	20MW	0MW

구분	운영 유지비용	전송 비용
자료: DeSantis, D. et al.(2021)와 Acaroğlu, H. and Márquez, F. P. G.(2022)
HVDC	설비용의 0.5%	40[$/MWh]

구분	ESS 도입 여부 및 목표 출력제어율
S1	도입(출력제어율: 3%)
S2	도입(출력제어율: 5%)
S3	미도입(현행 유지)

구분	총비용 (①+②+③+④)	HVDC 비용 (①)	발전 비용 (②)	ESS 설비비용 (③)	탄소배출 비용 (④)
S1	65,903	14,384	33,629	16,573	1,317
S2	60,080	14,416	33,982	10,356	1,326
S3	50,527	14,433	34,718	0	1,376

구분	총비용 (①+②+③+④)	HVDC 비용 (①)	발전 비용 (②)	ESS 설비비용 (③)	탄소배출 비용 (④)
S1	92,772	20,838	53,251	16,573	2,110
S2	87,469	20,771	54,006	10,356	2,156
S3	81,990	22,710	56,962	0	2,318