통합기후모형을 통한 우리나라 최적 탄소세 추정 연구
초록
통합기후모형을 통한 우리나라의 최적 탄소세 추정 연구는 아직까지 미비한 상태이다. 본 연구는 최근 벤치마크 통합기후모형으로 광범위하게 사용되는 Golosov, Hassler, Krusell, and Tsyvinski (2014) 모형을 국내에 적용하여 우리나라의 최적 탄소세를 추정하였다. 1955년 이후의 거시 및 기후변수들의 시계열 데이터를 이용하여 우리나라의 피해 계수를 추정하였으며 이를 Golosov, Hassler, Krusell, and Tsyvinski (2014) 모형의 최적 탄소세 공식에 적용하여 우리나라의 최적 탄소세를 도출하였다. 2019년 GDP 및 국내 총 탄소 배출량을 기준으로 추정된 벤치마크 모수 값 들을 적용한 결과 탄소 1톤당 최적 탄소세는 약 2,000원에서 14,000원 사이로 추정되었다. 본 연구의 결과는 추후에 기후변화대응 정책 수립 및 통합기후모형을 적용한 우리나라의 최적 탄소세 추정연구에 중요한 벤치마크 정보를 제공할 것으로 기대된다.
Abstract
Integrated Assessment Model (IAM) based studies on the optimal carbon tax in Korea are still lacking in the literature. This study aims to provide estimates for the optimal carbon tax in Korea by applying the IAM developed by Golosov, Hassler, Krusell, and Tsyvinski (2014). Damage functions in Korea are estimated using time series of macro and climate variables dating from 1955. We then apply those estimates into Golosov, Hassler, Krusell, and Tsyvinski (2014)’s optimal tax formula. Based on Korea’s 2019 gross domestic product (GDP) and level of carbon emissions, optimal carbon taxes are estimated to be between ₩2,000 and ₩14,000 per ton of carbon. Our results are expected to serve as a stepping stone for further IAM studies on a Korean optimal carbon tax.
Keywords:
Climate Change, Social Cost of Carbon, Integrated Assessment Model, Optimal Carbon Tax키워드:
기후변화, 탄소의 사회적 비용, 통합기후모형, 최적 탄소세I. 서론
점점 가속화되고 있는 지구온난화와 이에 따른 기후변화는 인류가 공통으로 직면한 가장 중요한 문제 중 하나라는 것에 대한 이견은 존재하지 않을 것이다. 지구온난화의 주범으로 인식되고 있는 탄소배출을 줄이기 위한 노력 또한 전 지구적으로 펼쳐지고 있다. 대부분의 선진국은 2050년 탄소중립 달성을 목표로 다양한 정책을 통한 탄소 저감 노력을 추진하고 있다. 우리나라도 예외는 아니다. 국가 온실가스 감축목표에 따르면 정부는 다양한 정책들을 통하여 2018년 대비 2030년 국내 온실가스 배출량을 35% 이상 감축하겠다는 의지를 표명하고 있다.
이와 더불어 기후변화 관련 국제협약 시 필연적으로 발생하는 무임승차 문제를 해결할 방안들도 심도 있게 논의되고 있다. 이미 유럽연합(EU)은 탄소 저감 노력을 소홀히 하는 국가의 수입품에 대한 관세(Carbon Border Adjustment Mechanism)를 2026년부터 도입하겠다고 공표하였으며 미국 의회도 EU와 유사한 탄소 국경세 도입을 추진하고 있다. 결국 우리나라는 대내외 모든 측면에서 탄소배출 감소라는 실질적인 압력을 받고 있는 것이다.
문제는 탄소배출 저감은 필연적으로 막대한 비용을 수반한다는 점이다. 이러한 상황 속에서 최적 탄소세 또는 탄소의 최적 사회적비용(Social Cost of Carbon, SCC)을 정확히 추정하는 것은 우리나라의 정책 입안자들에게 매우 중요한 정책적 과제라 할 수 있다. 우리나라에서의 최적 SCC는 최적 탄소배출 저감 목표를 설정하고 그에 필요한 최적화된 정책 수단을 선택하는데 핵심적인 정보이기 때문이다. 그뿐만 아니라 향후 우리나라가 직면할 수 있는 기후변화 관련 국제협상(탄소세 관련 협상 등)에서 불이익을 당하지 않기 위해 우리가 알고 제시해야 할 핵심적인 정보이기도 하다.
하지만 국내에서 우리나라의 최적 SCC에 대한 추정 연구는 현재까지 많이 존재하지 않는다. 일반적으로 해외 연구에서는 최적 SCC를 추정하기 위해 통합기후모형(Integrated Assessment Model, IAM)을 사용한다. 하지만 대부분의 국내연구는 IAM의 핵심 요소인 피해함수(damage function)를 추정하기보다는 그것이 외생적으로 결정된다고 가정하고, 탄소 관련 정책이 변화할 때 발생할 수 있는 여러 가지 거시경제변수의 변화를 경제적 피해 비용으로 산출하는 방식을 택했다. 하지만 이는 기후변화 관련 대응을 포함한 최적 자원의 배분 상태를 고려한 탄소의 사회적 비용이 아니기 때문에 진정한 의미의 최적 SCC를 추정한 연구로 보기에는 한계가 있다.
이러한 단점을 보완하기 위해 본 연구는 최근 해외 학계에서 IAM 벤치마크 모형으로 주로 활용되는 Golosov, Hassler, Krusell, and Tsyvinski (2014) 모형을 국내에 적용하여 우리나라에서의 최적 SCC를 추정하였다. Golosov et al.(2014) 모형이 최근 학계에서 주목받고 있는 이유는 이미 잘 알려져 있다. Nordhaus(1991)의 대표적인 IAM인 Dynamic Integrated Climate Economy(DICE)에서는 최적 SCC를 닫힌 해로 표현할 수 없고 오로지 수치적 방법(Numerical Method)으로만 추정할 수 있다는 단점이 있어서 정책 입안자들이 궁금해하는 탄소세가 후생에 미치는 영향의 채널을 규명하는 데 어려움이 있었다. 하지만 Golosov et al.(2014) 모형은 Dynamic Stochastic General Equilibrium(DSGE) 모형임에도 불구하고 모형구조에 관한 몇 가지 간단한 가정을 통해 최적 SCC를 간단한 몇 개의 모수들(시간할인율, 탄소순환계수, 총요소생산성(Total Factor Productivity, TFP)의 기후변화에 대한 민감도)로만 표현할 수 있다는 장점이 있다. 이는 앞에서 언급했던 탄소세 부과의 후생효과를 정성적으로 분석하는 도움을 줄 뿐만 아니라 기존의 DICE에 기초한 모형들에서 최적 SCC를 추정하는 데 필요했던 상세한 정보들(예를 들어, 미래 화석에너지 및 재생에너지 분야의 기술 및 경제적 중요성 예측, 그리고 미래의 기후변화 및 탄소 축적량에 대한 예측 등)에 대한 추정이 필요 없다는 의미이기도 하다.
Golosov et al.(2014) 모형을 통한 국내 최적 SCC 추정을 위해서는 피해계수(생산성의 온도 탄력성)와 탄소민감도계수(온도의 탄소 탄력성)의 추정이 핵심이다. 국내적 특성이 존재하는 피해계수는 1955년부터 2020년까지의 거시 및 기후변수 데이터를 사용한 시계열 분석을 통하여 추정하였다. 마지막으로 탄소민감도계수 또한 탄소배출이 지구 온도에 미치는 영향이 지구 전 지역에 걸쳐 거의 균등하다는 대다수의 기후과학 연구 결과를 바탕으로 Golosov et al.(2014)의 모수를 사용하였다.1)
이러한 모수들의 값을 사용하여 도출한 2019년 GDP 기준 연평균 탄소의 총 외부효과 비용은 약 3,000억 원에서 2조 7,000억 원 사이로 나타났다. 이를 탄소 1톤당 외부효과 비용으로 변환하면 2019년 GDP 기준으로 우리나라에서의 최적 SCC가 약 2,000원에서 14,000원 사이로 추정됨을 의미한다. 물론 이러한 추정값들은 일반적으로 Nordhaus가 사용하는 상대적으로 높은 시간할인율(β=0.985)을 사용했을 때 나타난 결과이다. 만약 Stern(2007) 리포트에서 주장되는 낮은 시간할인율(β=0.999)을 적용하면 위의 값들은 거의 10배 이상 증가하는 결과가 나타났다. 탄소의 연평균 총 외부효과 비용은 약 3조 5,000억 원에서 26조 원 사이로 나타나며, 1톤당 외부효과 비용은 19,000원에서 137,000원 사이로 나타났다.
본 연구는 다음과 같이 구성되어 있다. 제Ⅱ장에서는 선행연구들을 정리하였고 또 본 연구가 어떻게 기여할 수 있는지 설명하였다. 제Ⅲ장에서는 본 연구에서 사용된 모형을 요약하였다. 다음으로 제Ⅳ장에는 우리나라의 최적 SCC 추정을 위해 필요한 모수들을 추정하였다. 또한 이와 관련된 데이터와 방법론을 추가로 설명하였다. 제Ⅴ장에서는 우리나라의 최적 SCC를 추정하였으며 Stern(2007) 시간할인율을 사용한 강건성 검증을 수행하였다. 마지막으로 제Ⅵ장은 결과를 요약, 정리하였다.
Ⅱ. 선행연구 및 본 연구의 차이점
최적 SCC 또는 최적 탄소세에 관한 학계의 연구는 1970년대부터 활발해지기 시작했다. 물론 그 이전부터 환경세라는 개념의 논의는 있었지만 Nordhaus(1977)와 Baumol(1972)를 필두로 많은 경제학자가 지구온난화가 경제활동에 미치는 영향을 분석하기 시작했다. 1990년 초 Nordhaus가 IAM을 개발한 이후로 최적 SCC에 관한 논의는 구조모형을 통하여 본격적으로 추정되기 시작했다. 최적 SCC에 관한 좀 더 자세한 배경은 이미 많은 review 논문들에 나와 있다.
IAM을 통한 최적 SCC 추정연구는 전통적으로 Nordhaus(1992) DICE 모형에 바탕을 둔다. DICE 모형의 핵심적인 기여는 경제활동, 탄소배출, 그리고 기후변화가 미치는 부정적 외부효과를 일반균형 모형을 통하여 모두 내생적으로 도출하였다는 점이다. DICE 모형 이전의 연구들은 위 세 가지 내생변수들 중 하나는 외생변수로 간주하고 오로지 나머지 두 가지 변수들 간의 내생적 관계를 분석해 왔다는 측면에서 문제점을 가지고 있었다. 이러한 문제를 DICE 모형은 피해함수(damage function), 즉 기후변수의 변화가 어떻게 총요소생산성에 영향을 미치는지 보여주는 함수를 가정함으로써 풀어냈다. 이러한 가정을 통하여 기후변화의 부정적 외부효과를 고려한 최적 자원배분 상태를 도출하고 그것을 바탕으로 최적 SCC를 추정할 수 있다는 점이 DICE 모형의 핵심적 기여가 된 것이다.
물론 기후변화가 경제의 총요소생산성에 직접적으로 부정적인 영향을 유발한다는 DICE 모형의 가정은 매우 단순한 가정임을 인지하기란 몹시 어렵지 않다. 실질적으로 기후변화가 유발하는 부정적 외부효과는 무수히 많은 채널을 통하여 존재할 수 있기 때문이다. 따라서 최근 IAM 모형들은 피해함수와는 별도로 훨씬 더 내생적인 채널들을 고려하여 최적 SCC를 도출하는 연구들을 진행하고 있다. 기후변화는 총요소생산성뿐만 아니라 이민과 국제무역의 패턴변화에도 상당한 영향을 끼칠 수 있다는 많은 실증분석 논문들이 증명한다. Cruz and Rossi-Hansberg(2022)는 이러한 새로운 채널을 IAM에 추가하여 최적 SCC를 추정한 연구를 발표하였다. Acemoglu, Aghion, Bursztyn, and Hemous(2012)는 기후변화가 화석연료와 재생에너지 분야의 기술 발전을 내생적으로 결정할 수 있다는 채널을 추가하여 최적 기후변화대응 정책을 연구하였다. Nordhaus(2015) 및 Hémous(2016)은 기후변화대응 정책 수립 시 필연적으로 유발되는 무임승차 문제를 고려한 IAM을 개발하여 최적 탄소의 사회적 비용을 재추정한 연구도 제시하였다.
하지만 이러한 최근 IAM 모형들은 구조의 복잡성으로 인해 거의 대부분은 최적 SCC를 오로지 수치적 방법론을 통해서만 계산이 가능하다는 단점이 있다. 앞에서 언급되었던 것처럼 Golosov et al.(2014)는 이러한 문제점을 거시경제학계에서 널리 쓰이는 몇 개의 핵심 가정을 추가하여 해결하였다. 이는 그동안의 연구 결과들이 제공하지 못했던 방법론적인 장점들을 제공했다는 점에서 매우 큰 의미가 있다고 볼 수 있다. 문제는 Golosov et al.(2014) 모형을 통한 국내 최적 SCC 추정 연구가 매우 미흡하다는 것이다. 지금까지 대부분의 탄소의 사회적 비용 추정 국내연구는 주로 연산가능 일반균형(Computable General Equilibrium, CGE)모형을 활용해 왔다.2) 하지만 이러한 CGE 모형들은 부분균형모형이라는 한계로 인해 기후변화와 관련 대응 정책의 상호작용에 대한 내생적 도출이 불가능하다는 단점이 있다.
다행스럽게도 대략 10년 사이에 IAM 모형을 활용한 국내연구가 시작되고 있다. 필자들의 지식에 따르면 크게 두 가지 종류의 연구가 수행되었다. 첫째, 환경부(2009)에서 발간한 “우리나라 기후변화의 경제학적 분석”이 있다(전성우 외, 2010; 채여라・김용건・주광우・조현주・최성윤, 2012; 채여라・조현주, 2011). 위의 연구들은 Hope, C., Anderson, J., and Wenman, P.(1993)의 PAGE 모형을 채택했다는 특성이 있다. 또한 기존 DICE 종류의 모형들에서 고려하지 않은 지역적 특성을 IAM에 추가했다는 데 의의가 있다. 다만 PAGE 모형에서는 우리나라를 독립적인 지역으로 분석하기보다는 우리나라를 기타 국가에 포함하여 산출한 SCC에 가중치를 가해 한국에서의 탄소의 사회적 비용을 분석했다는 단점이 있다. 더 중요한 단점은 PAGE 모형 자체가 기후, 경제, 정책이 완전히 내생화가 되지 않은 부분균형 모형이란 점이다. 본 연구와 가장 밀접히 연결된 선행연구는 정국모・황다슬(2022)이다. 필자들의 지식에 따르면 정국모・황다슬(2022)은 국내 최초로 Golosov et al.(2014) 모형을 사용하여 제주도의 최적 탄소의 사회적 비용을 도출하였으며 이를 위해 제주도만의 피해함수 그리고 탄소민감도 계수를 따로 시계열 분석을 통하여 추정하였다. 제주도만의 지역적 특성을 고려한 최적 SCC 추정이라는 측면에서 의미가 있으나 여전히 글로벌 경제모형인 Golosov et al.(2014)을 소규모 지역에 적용했다는 한계가 존재한다. 본 연구는 제주도에 국한된 연구를 국내 전체로 확대하여 Golosov et al.(2014)의 글로벌 모형적 특성의 단점을 최소화하였고 피해함수 추정을 위한 데이터가 정국모・황다슬(2022)보다 훨씬 더 길어졌다는 장점이 있다. 글로벌 모형을 특정 국가에 적용하는 것에는 한계가 존재하나 그런데도 글로벌 모형을 사용하는 이유는 다음과 같다. 지역적 특성을 고려하는 모델을 사용하면 측정해야 하는 모수가 많아져 최종적으로 SCC를 구하기 어렵다는 단점이 존재한다. 또한, 미래의 기후변화 영향을 모형화하기 위한 관측값이 부족하여 불확실성이 높아질 수 있다. 따라서 본 연구는 글로벌 모형인 Golosov et al.(2014)을 처음으로 우리나라에 적용하여 기후변화 관련 거시피해 비용을 추정한 벤치마크로써 의미를 지닌다고 본다.
Ⅲ. 통합기후모형
1. 모형 및 주요 가정
본 연구의 기본 모형은 Golosov, et al.(2014)의 통합기후모형(GHKT 모형)의 축약본이며 정국모・황다슬(2022)이 사용한 축약버전과 동일하다. 따라서 모형에 대한 설명은 최대한 간결하게 등식 위주로 설명하기로 한다.
소비자의 동태적 효용과 최종상품생산자의 제약식은 아래와 같이 정의된다. 먼저 동태적 아래의 동태적 효용식에서 C는 소비를 의미하여, β는 시간할인율을 의미한다.
총 3가지(i =1,2,3)의 에너지 섹터가 존재하며 최종상품생산자의 인덱스는 0이라 가정한다i=0). 최종상품생산자의 자원 제약식은 일반적인 경우와 마찬가지로 다음과 같이 가정한다.
자원 제약식의 우변은 현재기의 소비(Ct)와 다음 기에 사용할 자본 스톡(Kt+1)을, 우변의 Yt는 최종상품과 감가상각 후 남은 자본을 의미한다. N0,t은 최종상품생산자의 노동 투입량을 의미하고 E0,t는 최종상품생산자의 에너지 투입 요소의 벡터를 의미한다. St는 대기 중 누적 탄소 축적량을 의미한다. 에너지 투입 요소(Ei,t)의 생산함수 또한 최종상품생산자의 생산함수와 유사한 형태를 지닌다고 가정한다.
각각의 에너지자원 매장량(Ri,t+1)도 다음의 동태 방정식을 따른다고 가정한다.
| (1) |
오일섹터는 한계생산비용이 ‘0’이라고 가정하고 석탄과 재생에너지 섹터는 아래와 같은 선형노동생산함수를 가진다.
Ai,t는 섹터 i의 TFP를 의미한다. 에너지 복합재(Et)는 CES 함수의 형태를 가진다.
| (2) |
위의 동태적 효용을 자원 제약식 하에서 극대화하는 사회계획자(social planner) 문제를 풀기 전에 다음 세 가지 가정을 추가로 적용한다. 우선 효용함수와 피해함수는 다음의 축약된 가정을 따른다.
첫 번째로 효용함수는 자연로그 함수로 가정한다. 두 번째로 대기 중 누적 탄소 축적량이 최종상품생산자의 생산함수에 영향을 미친다고 가정한다. 이때, 는 산업화 이전 누적 탄소 축적량을 의미하고, rt는 t기의 탄소배출이 산업화 이전의 탄소 배출량을 초과할 때 최종 생산을 얼마나 감소시키는지 측정하는 피해 계수를 의미한다. 즉, 피해 계수(rt)가 0보다 클 때, 현재기의 탄소배출(St)이 산업화 이전 탄소 배출량()을 초과하면 최종생산재인 F0,t가 감소한다.
세 번째 가정은 대기 중 탄소 축적량의 진화과정에 관한 것이다.
| (3) |
가정3은 대기 중 탄소 축적량이 과거로부터 배출되어온 탄소의 가중평균으로 결정됨을 의미한다.
2. 탄소의 사회적 비용
사회계획자(social planner) 문제는 다음과 같이 정의된다.
사회계획자는 이를 풀어서 최적 자원배분을 결정하게 된다. 탄소배출의 한계외부비용(Λi, t), 또는 총 SCC, 또는 피구세(Pigouvian Tax)를 아래와 같이 닫힌 해의 형태로 도출할 수 있다.
Golosov, et al. (2014)와 같이 가정 1, 2, 3과 시불변적(non-timevarying) 기후변화피해계수 를 가정하면 GDP 대비 탄소배출의 한계외부비용은 다음과 같이 오로지 모형의 상수들로 이루어진 간단한 닫힌 해의 형태로 도출된다.
| (4) |
위의 식이 본 모형의 핵심 방정식이다. 본 모형에서 도출된 GDP 대비 탄소의 사회적 비용은 오로지 세 가지 모수에 의해서 결정된다. 즉, 미래기후변화 피해의 현재 할인율 β, 탄소축적의 장기성을 나타내는 탄소순환 계수(ϕL, ϕ0, ϕ), 그리고 탄소 축적량이 얼마나 많은 TFP를 감소시키는지 결정짓는 계수 γ에 의하여 탄소의 사회적 비용이 결정된다. 이와 같은 사실은 타 IAM 모형들보다 더 적은 양의 정보를 통해 SCC를 유추할 수 있다는 장점이 있다. 다음 장에서는 모형에서 도출된 SCC를 국내에 적용하는 데 필요한 모수를 우리나라 데이터를 이용하여 추정(Ⅳ장)하고 그 모수를 바탕으로 대한민국의 여러 가지 기후변화 시나리오를 바탕으로 국내 기후변화 피해 비용을 최종적으로 추계(Ⅴ장)하기로 한다.
Ⅳ. 모수 추정
1. 시간할인율 및 탄소순환계수
첫 번째 주요 모수인 시간할인율은 정국모・황다슬(2022)와 같이 두 가지 할인율을 채택하였다. 우선 Nordhaus(1992)에서 사용된 상대적으로 높은 할인율 β=0.985을 사용하고 비교 대상으로 Stern(2007) 리포트에서 사용된 상대적으로 낮은 할인율 β=0.999도 사용하였다. 할인율은 기후변화의 피해액을 결정하는 주요 계수로 할인율이 높을수록 미래세대가 겪을 기후변화 피해액의 현재가치가 줄고 할인율이 낮을수록 피해액의 가치가 커진다. 즉, Nordhaus(1992)에서 사용하는 상대적으로 높은 할인율은 학계에서 많이 사용되는 할인율로, 이 할인율을 적용하게 되면 미래세대가 겪을 피해를 현재시장의 관점으로 할인하게 되는 것이다. 그러나 윤리적으로 미래세대가 받을 피해를 고려해 낮은 할인율을 적용한다면 그 피해액이 커지는 방향으로 추정할 수 있다. 이와 같은 주장을 하는 Stern(2007) 리포트는 상대적으로 낮은 할인율을 적용한다. 이에 본 연구는 두 가지 모두의 할인율을 적용하여 비교분석을 하였다.
두 번째 핵심 모수는 탄소순환계수(ϕL, ϕ0, ϕ)이다. 이러한 탄소순환계수들은 정국모・황다슬(2022)에서 설명된 것처럼 기후과학 분야에서 연구되고 도출된 계수들로서 글로벌한 특성이 잘 나타난다고 알려져 있다.3) 이러한 이유로 본 연구에서도 정국모・황다슬(2022)와 같이 GHKT 모형에서 이미 사용된 아래의 값들을 채택하였다.
2. 전국 피해함수 추정
우리나라의 최적 SCC 추정을 위해 필요한 가장 중요한 모수는 시불변적 피해계수(γ) 이다. 피해계수는 가정2에서 정의된 아래와 같은 지수함수의 계수로 정의된다.
피해계수(γ)는 현재기의 탄소배출(St)이 산업화 이전의 탄소배출량()을 초과할 때 전체 경제의 TFP를 얼마나 감소시키는지 측정하는 탄력성이라 할 수 있다.
본 연구에서는 정국모・황다슬(2022)와 동일한 방법으로 시계열 분석을 사용하여 피해계수를 추정하였다. 기존 연구에서 사용된 횡단면분석이나 패널분석 방법론에 대한 자세한 설명은 정국모・황다슬(2022)에 잘 설명되어 있다. 우선 다음의 최종생산자 생산함수 형태를 가정하였다.
Yt는 t기의 총생산량을 의미하고 Tt는 산업화 이전 온도 대비 t기의 온도 변화량, 그리고 Pt는 강수량 변화량을 나타내는 변수로 정의한다. 즉, 피해함수를 온도와 강수량의 다항함수로 가정한 것이다. 시계열이 변함에 따라 온도와 강수량 또한 변하지만, 정국모・황다슬(2022)와 동일하게 피해계수()는 시불변적이라고 가정하였다. 마지막으로 을 추정하기 위한 회귀방정식은 위의 생산함수를 차분한 아래의 차분 방정식을 채택하였다.
피해함수 추정을 위해 1955년부터 2020까지의 5개의 변수 Yt, Lt, Kt, Tt, Pt에 대한 시계열자료를 구축하였다. 실질 총생산(Tt)은 통계청, 『국민계정』에서 1955년부터 2020년까지의 자료를 사용하였다. 총노동투입(Lt)은 가장 긴 시계열자료를 사용하기 위해 국가통계포털, 『인구주택총조사』에서 1955년부터 2020년까지 5년 단위의 취업자 수를 내삽법을 통해 추정하여 사용하였다. 총자본스톡(Kt)은 박희석(2010)을 따라서 전통적인 영구재고법(Perpetual inventory method)을 이용해 추정하였다. 이를 위해 필요한 투자 변수(lt)는 국가통계포털, 『국민계정』에서 전국 총고정자본형성(Gross fixed capital formation)4)을 사용하였다. 영구재고법을 이용하여 총자본스톡을 추정하는 방법은 정국모・황다슬(2022)과 같기 때문에 자세한 설명은 생략하기로 한다. 총자본스톡은 초기 자본스톡을 이용해서 다음과 같은 자본형성식에 의해 계산되었다.
기온(Tt)과 강수량(Pt)은 국립기상과학원(2018)을 따라 전국 연평균 기온과 연강수량 추정 방법을 사용하였다. 기상자료개방포털에서 장기간 관측이 존재하는 강릉, 서울, 인천, 대구, 부산, 목포 총 6개의 관측지점의 일 최고기온과 일 최저기온(단위: ℃) 및 일 강수량(단위: m) 자료를 사용하였다. 전국 연평균기온을 추정하기 위해 관측지점의 일 평균기온을 사용하여 전국 평균을 구했고, 전국 연강수량은 대표 관측지점 연강수량의 평균으로 추정하였다. <표 1>은 이러한 방법으로 계산된 기후변수 값들을 포함한 모든 변수의 통계량을 보여준다.
이미 설명되었듯이 전국 피해함수 추정 회귀식은 다음과 같다.
εt는 오차항이다. 앞서 정의한 바와 같이 Tt와 Pt는 산업화 이전 대비 변화량이다. 먼저 산업화 이전 연도를 정의하기 위해 60년부터 80년까지 매 연도를 산업화 이전 연도로 정의하고 피해계수를 각각 추정해보았다. 그 결과 산업화 이전 연도를 55년부터 59년까지, 그리고 70년으로 정의했을 때 피해계수가 유의하게 나왔으며 그 결과는 <표 2>와 같다.
전국 피해계수 추정 결과 대부분 정성적으로 같은 양상을 보인다. 온도(Tt)는 산업화 기준 연도가 1959년인 경우를 제외하고 전부 총생산과 오목한 관계를 보인다. 또한 1959년을 제외한 모든 곳에서 온도 변수의 본항과 제곱항 모두 통계적으로 유의미한 값을 보인다. 이는 온도가 어느 특정 지점까지 상승하면 총생산이 증가하지만, 그 이상으로 온도가 높아지면 총생산이 감소한다는 의미이다. 예를 들어 1955년을 산업화 이전 연도로 정의한 경우, 이 전기와 온도의 차이 자체가 2.5℃ 증가 시 총생산의 경우 이 전기와의 성장률 차이 자체가 5.455%p 감소한다. 반면 강수량(Pt)의 제곱항의 경우 대부분 음의 결과를 보이지만 본항은 통계적으로 유의미하지 않은 결과를 보여주고 있다. 또한 총자본형성도 모든 연도에서 유의한 결과를 보여주고 있지만 총노동투입은 통계적으로 유의미하지 않은 결과를 보여주고 있다.
마지막으로 전국 피해계수(γ)는 온도의 함수로 표현된 피해함수(D(T))와 탄소의 함수로 표현된 온도함수(T(S))의 조합으로 추정할 수 있다. 이때 온도의 함수로 유도한 피해함수 추정식을 가정2에서 정의한 대로 탄소배출량의 함수(T(S))로 전환하기 위해 GHKT 모형에서 사용되었던 아래의 관계를 설정하였다.
는 산업화 이전 대기 중의 이산화탄소 축적량을 나타내고, Tt는 산업화 이전 대비 t기의 온도 변화량을 의미한다. 위의 관계식은 산업화 대비 이산화탄소를 배출함에 따라 평균적으로 지구의 온도가 얼마나 증가하는지 보여준다. 탄소배출에 따른 온도 변화는 지구 전 지역에 걸쳐 효과가 있으므로 본 연구에는 전국 탄소민감도(λ)와 산업화 이전 대기 중의 이산화탄소 축적량()을 따로 추정하지 않고 GHKT모형에서 사용된 값들을 채택하였다.
위의 값들을 채택하면, Tt와 St의 관계식에 따라 t기의 탄소배출량(St)이 산업화 이전 이산화탄소 축적량의 두 배가 되면 t기의 온도가 산업화 이전 온도에 비해 3℃ 증가한다.
따라서 피해계수(γ)는 산업화 이전 대비 3℃ 증가를 가정하고 D(T)와 T(S) 함수를 결합하여 다음과 같은 방정식을 통해 도출하였다.
위의 방정식으로 측정한 피해계수는 <표 3>과 같다.
3) 장에서 보고된 것처럼 강수량은 피해함수에 통계적으로 유의한 영향을 끼치지 않아 피해함수 정의역의 원소로 포함하지 않았다. 또한 산업화 이전 기준 연도가 1959년일 때 온도 변수가 통계적으로 유의하지 않아 피해계수를 측정하지 않았다. 피해계수 측정 결과 1956년의 피해계수는 음수값을 갖는데 이는 1956년의 연평균 온도가 다른 기준 연도보다 특히 낮기 때문인 것으로 추정된다. 즉, 1956년을 산업화 이전 연도라고 정의했을 때, 온도가 산업화 이전 온도 대비 3도 상승해도 총생산이 감소하지 않고 오히려 증가한다는 의미이다. 표에 나타나 있듯이 산업화 이전 연도를 어떻게 정의하느냐에 따라 피해계수는 크면 약 8배 정도 차이 나는데, 이는 시계열자료가 짧아 피해계수의 변화가 큰 것으로 본다. 본 연구에서는 1955년부터 모든 변수의 데이터가 존재하는 것을 감안하여 1955년의 피해계수를 벤치마크로 삼기로 한다. 따라서 도출된 전국 피해계수는 γ=6.317ㆍ10-5로 추정되었다. 이는 GHKT 모형의 벤치마크 글로벌 피해계수인 γ=2.38ㆍ10-5 보다 약 세 배가량 높은 수치임을 확인할 수 있다.
마지막으로, 추정된 피해함수를 통해서 기후변화가 TFP에 얼마나 큰 피해를 유발하는지 추론해 볼 수 있다. <그림 1>은 <표 2>에 추정된 피해계수(γ)를 바탕으로 산업화 이전 대비 평균온도 변화가 섭씨 0도에서 3도까지 증가하면 연평균 TFP가 얼마나 감소하는지 보여주고 있다.
<그림 1>에서 볼 수 있듯이 연평균 총요소생산성 감소량은 산업화 대비 평균온도의 증가량에 반비례함을 알 수 있다. 이러한 특징은 GHKT 모형과 정성적으로 일치하는 직관적인 결과이다. 모형에서의 피해함수가 모두 지수함수의 형태로 가정되기 때문이다. <표 4>는 IPCC 및 UN의 기후변화 관련 목표인 산업화 대비 섭씨 1.5도 이내 증가를 적용했을 때의 TFP 피해를 <표 3>에서 추정된 각 피해계수로 보여주고 있다. 본 모형의 벤치마크 피해계수인 γ=6.317ㆍ10-5를 사용했을 때 산업화 대비 기온이 파리기후협약 목표치인 1.5℃ 증가하면 국내 연평균 TFP가 약 1.5% 감소할 것으로 예측된다.
Ⅴ. 탄소의 사회적 비용
1. 우리나라에서의 최적 SCC 추정
GDP 대비 총 SCC를 도출하기 위해 IV 장에서 추정된 모수값들을 GHKT 모형의 최적 SCC 공식인 식(4)에 적용하였다. <표 2>를 기반으로 추정된 피해계수(γ)값을 벤치마크로 사용했다. 시간할인율은 Nordhaus 할인율인 β=0.985를 사용하였으며, 탄소순환계수들(ϕL, ϕ0, ϕ)은 IV 장에서 추정된 값을 사용하였다. 최적 SCC를 추출하기 위해 2019년의 명목 GDP(약 1924.5조)를 식(4)에 적용하였으며 탄소 1톤당 SCC 추정을 위해 2019년 기준 대한민국의 총 탄소배출량(약 1.89억 톤)을 사용하였다. 아래의 <표 5>에 결과가 정리되어 있다.
벤치마크 피해계수(γ)를 사용하여 추정한 전국 SCC는 약 2조 6,413억 원으로 나타났다. 이를 탄소 1톤당 SCC로 변환하면 탄소배출의 거시피해 비용은 약 14,000원으로 추정되었다. 참고로 이는 최근 한국에서 1톤당 탄소배출권의 가격이 약 1만 원대와 3만 원대 사이에서 거래되고 있음을 고려할 때 크게 시장가격과 다르지 않다는 것을 함의한다. 다만 기존의 해외 연구 결과에서 도출된 1톤당 최적 탄소세와 비교해보았을 때는 상대적으로 적은 수치임을 알 수 있다. Nordhaus and Boyer(2000)에서는 1톤당 최적 탄소세가 미화로 30불, Golosov et al.(2014)에서는 미화로 약 57불 정도로 나왔다. 기본적으로 Golosov et al.(2014)에서는 글로벌 단위의 GDP와 글로벌 단위의 피해계수(γ)를 추정하여 글로벌 SCC를 추정했지만, 본 연구에서는 우리나라만의 피해계수와 GDP를 이용해 추정했기 때문에 기존의 연구 결과와 다른 결과가 나온 것으로 볼 수 있다.
2. 강건성 검증
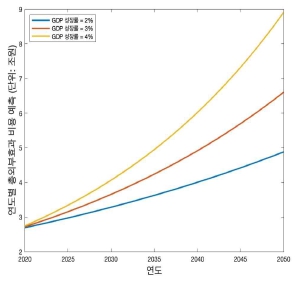
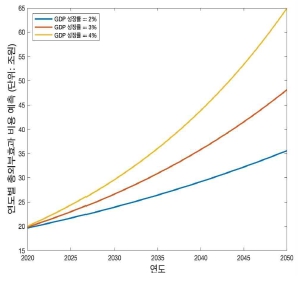
이미 잘 알려져 있다시피 통합기후모형에서 시간할인율은 SCC를 추정하는 데 핵심적인 역할을 한다. 직관적으로 미래에 기후변화로 인해 발생할 피해 비용을 현재가치로 환산할 때 중요한 역할을 하기 때문이다. 윤리적으로 미래세대가 겪을 피해를 현재보다 낮게 추정하는 것은 올바르지 않다는 이유로 많은 기후경제학자는 상대적으로 굉장히 낮은 할인율을 적용해야 한다고 주장한다. 하지만 이러한 방법은 통합기후모형의 기초라 할 수 있는 외생적 성장모형에서 도출되는 이자율을 현실 데이터로 맞추는 데 많은 어려움이 있어서 사용하지 말아야 한다는 주장도 존재한다. 이러한 논쟁을 잘 나타내주는 Stern(2007)과 Nordhaus(1992)라 하겠다. 본 연구에서는 이 두 가지 방법론을 모두 적용하였다. 1. 장에서는 학계에서 상대적으로 더 널리 사용되는 Nordhaus 할인율(β=0.985)을 적용하였다. 이번 장에서는 Stern 할인율(β=0.999)을 적용하여 추정한 탄소배출 관련 외부효과 비용 및 예측을 보고하도록 한다. 결과는 <그림 2> 그리고 <표 6>에 나타나 있다. 추정 방법은 기존과 같고 오로지 시간할인율만 더 높게(β=0.999) 적용되었다.
<표 5>와 <표 6>을 비교해보면 Stern 할인율을 적용했을 때, 총 SCC와 1톤당 SCC 모두 약 10배가량 증가한 것을 관찰할 수 있다. 이는 Nordhaus(2000)이나 Golosov et al.(2014)에서 Stern 할인율을 적용했을 때 나타나는 최적 SCC의 증가 비율과 유사한 패턴을 보인다. 참고로 두 논문 모두에서 Stern 할인율을 적용했을 때 최적 탄소세의 가격은 미화로 약 250불에서 500불의 범위에서 추정되었다. 미래의 기후변화 관련 피해 비용 예측치도 <그림 2>와 <그림 3>을 비교해보면 알 수 있듯이 Stern 할인율을 적용하면 약 10배가량 증가하는 것으로 나타난다.
Ⅵ. 결론
탄소의 외부효과 비용 또는 최적 SCC가 정확히 어느 정도 수준인지 파악하는 것은 전 세계적으로 가장 중요한 정책과제 중 하나이다. 이미 많은 선진국과 국제기구들은 다양한 종류의 IAM을 통하여 나라별로 최적 SCC를 추정하고 있으며 그에 상응하는 탄소 가격을 다양한 방법으로 부과하고 있다. 이러한 국제적 추세에도 불구하고 아직 통합기후모형을 통한 기후변화의 종합적인 피해 비용 산정은 국내에서 미흡한 상태이다. 탄소배출로 인한 사회적 비용 추정은 최적 기후변화대응 정책 수립뿐만 아니라 향후 급속하게 늘어날 국제 기후변화 관련 협상을 대비하기 위한 필수 정책과제라는 측면에서 우려하지 않을 수 없는 상황이다.
따라서 본 연구는 국내에서 최초로 최신 Golosov et al.(2014)의 IAM 모형을 통하여 우리나라에서의 최적 SCC를 추정하였다. 2019년 GDP 기준으로 국내에서 탄소의 총 외부효과 비용은 연평균 약 3,000억 원에서 2조 7,000억원 사이로 나타났다. 탄소 1톤당 최적 SCC 또한 2019년 GDP 기준으로 약 2,000원에서 14,000원 사이로 추정되었다. 다만 Nordhaus and Boyer(2000)에서는 탄소 1톤당 최적 SCC로 30불, Golosov et al. (2014)는 약 미화로 57불로 추정되었으며, 본 연구에서 추정한 결과는 기존 해외 연구보다 상대적으로 작은 수치임을 알 수 있다. 미래세대가 겪을 피해를 고려하여 미래에 기후변화로 발생할 피해를 낮은 시간율(β=0.999)를 적용하여 현재가치로 계산하면 위의 값들은 거의 10배 이상 증가하는 결과도 나타났다. 정확하게 2019년 GDP 기준으로 탄소의 연평균 총 외부효과 비용은 약 3조 5,000억 원에서 26조 원 사이로 나타나며, 1톤당 외부효과 비용도 19,000원에서 137,000원 사이로 나타났다.
본 연구에서 추정된 우리나라에서의 탄소의 사회적 비용의 한계점도 물론 존재한다. 근본적으로 Golosov et al.(2014) 모형이 지역적 특성을 고려하지 못한 글로벌 모형이기 때문이다. 탄소배출로 인한 기후변화가 지역별로 다르게 나타난다는 사실은 이미 기후 과학계에서 잘 알려져 있다. 추후 연구에서는 우리나라의 특성에 맞는 탄소민감도계수를 도출하는 것이 필요하다. 기후변화 현상 중 기온상승 외에 해수면 상승, 극한기상(extreme weather)의 빈도 증가, 생물의 다양성 감소 등이 거시경제에 미치는 비용을 고려하지 못한다는 점도 중요한 단점이다. 이러한 영향을 추가로 고려한다면 본 연구에서 추정된 국내에서 탄소의 사회적 비용은 충분히 과소평가 되었을 가능성이 있는 것이다. 이와는 반대로 Golosov et al. (2014) 모형이 기후변화로 인한 에너지산업 분야의 내생적 기술 발전을 고려하지 못한다는 사실은 본 연구에서 추정된 탄소의 최적 SCC가 과대평가 될 수 있음을 의미하기도 한다. 기후변화 자체가 신재생 에너지 분야의 기술혁신을 증대시킬 수 있기 때문이다. 이러한 모든 한계점은 앞으로 국내에서 탄소의 최적 SCC 추정연구가 보완하고 추가해야 할 중요한 과제일 것이다.
Acknowledgments
본 논문은 2022년 대한민국 교육부와 한국연구재단의 인문사회분야 신진연구자지원사업의 지원을 받아 수행된 연구임(NRF-2022S1A5A8052552).
References
- 국립기상과학원, 2018, 『한반도 100년의 기후변화』, 제주: 국립기상과학원.
-
권오상・강성원・이승호, 2017, “한국형 상・하향 통합모형을 이용한 농업 부문의 온실가스 감축 비용 추정,” 『환경정책』, 25(2), pp.61-85.
[https://doi.org/10.15301/jepa.2017.25.2.61]

- 김용건 외, 2015, 『온실가스 감축정책 평가를 위한 환경경제모형 개발・운용(II)』, 세종: 한국환경정책・평가연구원.
- 박희석, 2010, “우리나라 주요 시・도의 총요소생산성 추정,” 『서울도시연구』, 11(4), pp. 1-13.
- 오형나・홍종호, 2022, “디지털 전환의 기후효과: 현황과 전망,” 『한국경제포럼』, 14(4), pp.1~24, https://kiss.kstudy.com/Detail/Ar?key=3930717, .
- 전성우 외, 2010, “기후변화 통합영향평가모형 체계 개발: 정책연계모형개발을 중심으로,” 세종: 한국환경정책・평가연구원.
- 정국모・황다슬, 2022, “통합기후모형을 통한 제주도의 기후변화 피해 비용 추정,” 『경제학연구』, 70(2), pp.5-36.
- 채여라・김용건・주광우・조현주・최성윤, 2012, “우리나라 기후변화의 경제학적 분석(III),” 세종: 한국환경정책・평가연구원.
- 채여라・조현주, 2011, “기후변화 적응대책 우선순위 평가 방법론 분석,” 세종: 한국환경정책・평가연구원.
- 환경부, 2009, 『한국 기후변화 평가 보고서』, 세종: 환경부.
-
Acemoglu, D., Aghion, P., Bursztyn, L. and Hemous, D., 2012, “The environment and directed technical change,” American economic review, 102(1), pp.131-66.
[https://doi.org/10.1257/aer.102.1.131]

-
Archer, D., 2005. “The Fate of Fossil Fuel CO2 in Geologic Time,” Journal of Geoph-ysical Research, 110(C9), 2005
[https://doi.org/10.1029/2004JC002625]

-
Archer, D. et al, 2009. “Atmospheric Lifetime of Fossil Fuel Carbon Dioxide,” Annual Review of Earth and Planetary Sciences, 37(1), pp.117-34.
[https://doi.org/10.1146/annurev.earth.031208.100206]

- Baumol, W.J., 1972. “On taxation and the control of externalities,” The American Economic Review, 62(3), pp.307-322, https://www.jstor.org/stable/1803378, .
-
Cruz Álvarez, J. L.,, and Rossi-Hansberg, E. 2022. “Local Carbon Policy,” NBER Working Paper w30027.
[https://doi.org/10.3386/w30027]

-
Golosov, M., Hassler, J., Krusell, P., and Tsyvinski, A., 2014. “Optimal Taxes on Fossil Fuel in General Equilibrium,” Econometrica, 82(1), pp.41-88.
[https://doi.org/10.3982/ECTA10217]

-
Hémous, D., 2016. “The dynamic impact of unilateral environmental policies.” Journal of International Economics, 103, pp.80-95.
[https://doi.org/10.1016/j.jinteco.2016.09.001]

-
Hope, C., Anderson, J., and Wenman, P., 1993. “Policy Analysis of the Greenhouse Effect: An Application of the PAGE Model,”Energy Policy, 21(3), pp.327-38.
[https://doi.org/10.1016/0301-4215(93)90253-C]

- Nordhaus, W., 1977. “Economic growth and climate: the carbon dioxide problem,” The American Economic Review, 67(1), pp.341-346, https://www.jstor.org/stable/1815926, .
-
Nordhaus, W., 1991. “To slow or not to slow: the economics of the greenhouse effect,” The economic journal, 101(407), pp.920-937, https://www.jstor.org/stable/2233864, .
[https://doi.org/10.2307/2233864]

-
Nordhaus, W., 1992. “An Optimal Transition Path for Controlling Greenhouse Gases,” Science 258(5086), pp.1315-19, https://www.jstor.org/stable/2880417, .
[https://doi.org/10.1126/science.258.5086.1315]

-
Nordhaus, W., 2015. “Climate clubs: Overcoming free-riding in international climate policy,” American Economic Review, 105(4), pp.1339-70.
[https://doi.org/10.1257/aer.15000001]

- Nordhaus, W.D. and Yang, Z., 1996. “A regional dynamic general-equilibrium model of alternative climate-change strategies,” The American Economic Review: 741-765, https://www.jstor.org/stable/2118303, .
-
Nordhaus, William and Joseph Boyer. 2000. Warming the World: Economic Modeling of Global Warming, MIT press, Cambridge, MA.
[https://doi.org/10.7551/mitpress/7158.001.0001]

-
Stern, N., 2007. Stern Review: The Economics of Climate Change, UK
[https://doi.org/10.1017/CBO9780511817434]

- 국가통계포털, http://kosis.kr, .
- 기상자료개방포털, http://data.kma.go.kr, .
곽민정: 서강대학교 경제학과 석사과정 대학원생(kmj4746@sogang.ac.kr).
정국모: 서강대학교 경제학과 부교수(kmjung@sogang.ac.kr).