오염물 모형을 이용한 소득그룹별 환경원단위 효율의 비교
초록
본 연구의 목적은 오염물 모형을 이용하여 환경원단위효율 (EIE: environmental intensity efficiency)을 측정하고 이를 전통적인 환경원단위와 비교하여 보고자 함이다. 연구방법은 확률변경분석(SFA)에 기초한 생산효율과 환경효율의 동시모형을 사용하여 환경원단위효율을 추정하고 기존의 전통적 환경원단위와 비교한다. CO2 배출량 추정 식에서 노동, 화석에너지, 산출물 등은 1% 유의수준에서 유의적이고 정(+)의 부호를 보여주었다. 세 변수 중 화석에너지의 추정 계수가 0.795로 다른 변수보다도 온실가스 증가에 더 영향을 주는 것으로 나타났다. CO2 배출량에 대한 환경효율은 완만하지만 매년 평균 0.5%의 수준으로 향상되는 추이를 보여주고 있다. 환경효율은 고소득국가(G2그룹), 저소득국가(G5그룹), 하위중간소득(G4그룹) 등의 순서로 높게 나타났다. 생산효율의 경우도 매년 일정하게 증가하는 형태를 보였는데 국가별로는 고소득국과 OECD의 순서로 높았다. 환경효율과 생산효율로 측정한 환경원단위 효율도 역시 완만하지만 매년 증가하는 형태를 보였다. EIE의 효율은 전통적 원단위 효율과 차이를 보였다. 나아가 소득그룹에서 나타난 이질적 국가들을 재분류하는 평균분산접근을 사용하였을 때 EIE는 4개 그룹에서 뚜렷한 차이를 보여주었다.
Abstract
This study attempts to estimate environmental efficiency and production efficiency using a cost function model considering undesirable outputs and then compares environmental intensity efficiency (EIE) determined using these two efficiencies with conventional environmental intensity. The EIE was estimated using the simultaneous model of production efficiency and environmental efficiency based on Stochastic Frontier Analysis (SFA) and then compared against the environmental intensity determined in the traditional way. Considering the estimation of CO2 emissions, labor, fossil energy, and output are positively and significantly related to CO2 emissions at the 1% level. Fossil fuels have an estimated coefficient of 0.795, indicating a more significant impact on greenhouse gases than other variables. The CO2 emissions are not particularly efficient, but they are increasing by about 0.5 percent per year. The most environmentally efficient countries are, in order, high-, low-, and lower-middle-income countries. There is also an increasing trend in production efficiency yearly, with the highest being in the high-income and OECD (Organisation for Economic Co-operation and Development) groups, respectively. The EIE, calculated from production and environmental efficiency, is also rising. EIE values are highest in high-income countries due to their higher production efficiency and environmental efficiency. Conversely, OECD countries have the lowest EIE as a result of their high production efficiency combined with low environmental efficiency. Our EIE results differ significantly from the environmental intensity results and rankings calculated by the traditional method.
Keywords:
environmental efficiency, environmental intensity efficiency, environmental intensity, income level groups, mean-variance classification method키워드:
환경효율, 환경원단위 효율, 환경원단위, 소득그룹, 평균분산접근I. 서론
전 지구적으로 지구온난화가 초래할 재난으로 온실가스 저감은 이제 국제적으로 피할 수 없는 각 국가의 중대한 현안 과제가 되고 있다. 한국도 기후변화에 관한 정부간 협의체(IPCC)의 국가온실가스감축목표(NDC: Nationally Determined Contribution)에서 자유로울 수 없다. 한국은 2030년까지 1.70억 톤을 감축하는 계획을 IPCC에 제출했다가 미흡하다는 판정을 받고 2018년 대비 40%를 감축하는 안을 수정 제출하였고 지난 2021년 말에는 2050년 탄소중립계획을 발표한 바 있다. 이제 국가적으로 2050년까지 약 30년 정도의 기간에 온실가스를 2018년 기준 7.28억 톤에서 2050년에 0.80~1.17억 톤까지 배출량을 축소해야 하는 부담을 지게 되었다.1)
온실가스는 주로 화석에너지 사용으로 발생함으로 온실가스 감축은 에너지원을 화석에너지에서 신재생에너지로 전환하거나 또는 온실가스 분해 및 제거 기술을 통해 달성할 수 있다. 그러한 분해나 구축기술은 지금 개발 중이어서 현 단계에서는 당장 활용하기에는 한계가 있다. 따라서 현재 주된 통로는 신재생에너지로 에너지 전환을 통하여 온실가스를 감축해야 하는데 현재 한국이 전체 1차 에너지에서 신재생에너지가 차지하는 비중이 2019년 기준 2.31%로 10% 이상인 주요 선진국과 비교하면 매우 작다.2) 전원별 신재생에너지의 발전 비중을 주요 선진국과 비교하면 절대비중의 격차는 더 크게 난다.3) 현재 2% 초반의 신재생에너지 비중을 30년 이내에 약 50%로 늘린다는 목표는 결코 쉽지 않다.4) 한국은 국토 대부분이 산지이기 때문에 태양광과 풍력의 설치단가를 낮추기 어렵고 날씨 등의 여건도 좋지 않다. 나아가 온실가스를 저감하기 어려운 상황으로는 산업구조가 제조업 비중이 약 30% 수준으로 선진국 10~20%보다 높고 에너지 다소비 산업으로 구성되어 있다는 점이다. 이런 상황에서 한국의 탄소중립의 이행 기간은 30년이란 한 세대 만에 달성해야 하는 상황에 직면해 있다.
에너지 전환을 급속히 추진할 경우, 기존 화석에너지 발전소 등은 좌초자산이 될 뿐만 아니라 국민경제의 생산공정과 소비에서 전환비용이 심각하게 발생할 것으로 예견된다. 이처럼 2050 탄소중립의 과제는 경제일변도가 아닌 실질적인 환경과 경제의 지속가능성을 반영한 성장을 이루지 않으면 안 된다는 것을 말한다.
따라서 전통적으로 경제학이 중요시하는 경제적 생산성(산출/투입)에 기초한 생산효율뿐만 아니라 환경효율이 동시에 중요한 시대가 되었다. 원래 환경효율성은 최소오염물을 실제 오염물로 나누어서 정의된다. 이 환경효율성의 한계는 제레미 레프킨(2012)이 지적하듯이 경제적 생산성을 고려하지 못할 뿐만 아니라 경제적 생산성에 대비한 환경생산성(산출물/오염물)을 보여주지 못한다. 따라서 본 연구에서는 에너지 효율을 보는 대표적 지표로 에너지원단위(에너지사용량/GDP)를 사용하듯이 이를 결합한 환경원단위(오염물 배출량/GDP)를 사용하여 환경원단위 효율(EIE: environment intensity efficiency)을 측정하고자 한다.5) EIE는 최소환경원단위/실제환경원단위=(오염량/산출량)*/(오염량/산출량)를 말한다. 여기서 오염물은 지구온난화문제의 주범인 온실가스 즉 이산화탄소를 가리킨다. 이는 경제성장 속에서 탄소중립을 실현해야 하는 상반된 목표를 동시에 효과적으로 달성하는 지표로서 활용될 수 있다.
지금까지 전통적 환경원단위가 전반적인 경제의 환경적 건전성을 보여주는 지표로는 활용되어 왔다. 그러나 전통적인 환경원단위는 그 한계를 갖는다. 즉, 환경원단위를 구성하는 분자의 오염물이 많이 배출되어도 분모의 산출물(GDP)이 아주 크다면 환경원단위가 효율적이라고 간주할 수 있는 문제점이 있다. 나아가 환경원단위는 생산의 최종결과물로서 오염물과 산출물을 제시할 뿐이고 경제 구조가 암시하는 생산 과정의 환경효율을 보여주지 못한다. 무엇보다도 생산 단위가 얼마나 많은 오염물을 줄여야 하고 앞으로 저감이 필요한지에 대한 객관적인 목표를 제시해 주지는 못한다. 단지 비교 대상이 되는 생산단위에 비하여 환경원단위가 높고 낮음만을 보여주고 있다. 이처럼 본 연구는 전통적인 환경원단위가 환경과 경제의 지속가능성과 환경적 효율성을 보여주는 데에는 한계가 있다는 점에서 출발한다. 즉, 환경원단위(CO2/GDP)는 현재 오염원단위의 적정수준이나 최소화의 달성여부를 보여주지는 못한다. 이와 반대로 EIE를 사용하면 이를 보여줄 수 있다는 장점이 있다.6)
따라서 본 연구의 목적은 오염물을 종속변수로 두고 산출물을 설명변수로 포함한 오염물 모형을 이용하여 환경효율과 생산효율을 추정함으로써 EIE를 측정하고자 함이다. EIE의 추이를 166개국으로 다 표시하기 어려우므로 5개 소득 그룹으로 나누어서 결과를 제시할 것이다. 추가로 EIE를 전통적인 환경원단위와 비교해 볼 것이다. 나아가 5개 소득그룹에서 나타난 이질적 국가들을 재분류하는 평균분산접근을 사용하여 5개 소득그룹에서 나타나는 국가별 이질성을 동질적인 4개 그룹으로 재분류하여 결과를 비교해 볼 것이다.
지금까지 확률변경분석(SFA: stochastic frontier analysis)에 기초하여 환경효율을 측정한 연구는 타 분야에 비하여 그렇게 많지 않다. Reinhard 등(1999; 2000; 2002), Cuesta 등(2009), Herrala and Goel (2012), Zhou 등(2011), Zhou 등(2015), Duman and Kasman (2018), Bai 등(2019), Hsiao 등(2019), Bibi 등(2021) 등이 SFA접근으로 오염물에 대한 환경효율성을 연구하였다. 선행연구는 확률변경거리함수, 생산함수를 이용한 환경효율의 측정 등을 중심으로 대별할 수 있다.
첫째, 확률변경거리함수를 사용하여 환경효율을 측정한 연구로는 Cuesta 등(2009), Herrala and Goel(2012), Zhou 등(2011), Duman and Kasman (2018)가 있다. Kang and Kang(2022)은 SFA접근으로 에너지 효율과 에너지원단위 효율을 측정한 바 있다. 여기서 Herrala and Goel (2012)의 비용접근 모형을 제외하고는 대부분 선행연구들은 주로 투입접근 환경모형을 사용하였다. 이들 중 특히 Cuesta 등(2009), Duman and Kasman(2018) 등은 확률변경거리함수를 쌍곡선 모형과 결합하여 환경효율을 측정한 연구를 시도하였다. 한편, Zhou 등(2012), Hsiao 등(2019) 등은 확률변경함수를 사용하여 에너지효율을 측정하였다. 한편, Kang and Kang(2022)은 투입물거리함수에서 거리함수의 동차성을 이용하여 에너지원단위를 종속변수로 두고 확률변경분석을 통하여 직접 에너지원단위 효율을 측정한 것이다. 본 연구는 환경원단위 효율을 측정하기 위하여 생산효율과 환경효율을 동시에 측정하는 확률변경분석의 오염물 모형을 이용한다는 점에서 차이점이 있다.
둘째, 생산함수를 이용한 환경효율의 선행연구는 Reinhard 등(1999, 2000, 2002), Zhou 등(2015), Bai 등(2019), Bibi 등(2021) 등을 들 수 있다. 특히 Reinhard 등(1999; 2000; 2002)은 생산함수에서 산출물을 종속변수로 두고 오염물을 설명변수로 사용하여 환경효율을 측정하였다. Reinhard(2002)는 환경효율을 측정한 후 Tobit모형으로 그 영향요인을 분석하였다. Zhou 등(2015), Bai 등(2019), Bibi 등(2021) 등은 Reinhard 등(1999; 2000; 2002)의 방법으로 환경효율을 농업 등에 적용한 연구들이다.
국내적으로 EIE관련 선행연구는 김광욱 등(2012)이 있는 데 이들은 SFA가 아닌 확률오차를 고려하지 않는 선형계획방법을 사용하였다. 이 논문은 개별오염원단위를 통합한 통합오염원단위지수를 사용하였고 일종의 여러 오염물과 산출물을 합친 종합 오염원단위를 의미한다. 본 연구에서 사용한 실제오염원단위에 대한 최소오염원단위의 상대적 비율인 오염원단위 효율성과는 차이가 있다. SFA를 사용한 환경효율의 국내연구로는 공지영 등(2016), 강상목(2017), 김길환 등(2019), 김길환(2020)이 있다. 그 중 강상목(2017)은 확률변경분석을 에너지효율에 적용한 연구이다. 공지영 등(2016), 김길환 등(2019), 김길환(2020)은 이산화탄소를 사용한 환경효율을 측정하였다. 그러나 지금까지 SFA 방식을 사용하여 EIE 측정을 시도한 연구는 거의 찾을 수 없다.
선행연구의 한계점으로는 환경효율을 측정한 연구들은 많이 존재하지만, 환경효율은 오염물과 실제오염물의 비율만 보여주므로 경제의 생산기술효율은 동시에 보여주지 못한다. 그러므로 환경과 경제의 지속가능성을 함께 보여주려면 오염물과 GDP 비율로 제시되는 환경원단위를 기초로 원단위효율을 측정하고 관리할 필요가 있다. 본 연구에서는 SFA접근에 기초하여 Herrala and Goel(2012)과 같이 비용접근의 오염물 추정을 통하여 환경효율과 생산기술효율을 동시에 측정한다는 점에서 선행연구와 차별된다.
따라서 본 연구에서는 전통적인 환경원단위가 존재하지만 ‘환경원단위가 효율성을 대표하는 지표인가?’에 대한 의문을 제기한다. 본 연구는 환경원단위는 환경원단위 효율과 다를 것이라는 가설을 설정한다. 특히 선행연구에서 생산효율, 환경효율을 각각 측정하였으나 이에 기초한 환경원단위 효율을 시도하지는 않았으므로 본 연구는 한 함수에서 두 효율을 동시에 측정하는 모형을 이용하여 환경원단위 효율을 측정하고자 한다.
Ⅱ.이론모형
본 연구에서는 비용접근의 확률변경함수를 사용하여 환경효율(EE: environmental efficiency)과 생산효율(TE: technical efficiency)을 동시에 추정하여 EIE를 도출하는 방법을 소개하고자 한다.7) 본 연구는 환경오염원단위 효율 추정에 필요한 오염물 모형을 도입할 것이다.8) 확률변경함수에 기초한 오염물의 환경효율은 다음과 같이 정의된다, 즉,
| (1) |
여기서 환경효율은 실제오염물(W)에 대한 최소오염물(W*)로 정의한다. 환경효율을 θ로 두면 최소오염물(W*)은 θW가 된다. θ는 환경효율로 W를 최소화시킨다.
다음으로 산출물의 생산효율은 다음과 같다.
| (2) |
생산효율(TE)은 실제산출물을 최대산출물로 나눈 것으로 정의한다. 생산효율을 δ로 두면 최대산출물(y*)은 y/δ가 된다. 그러므로 δ(=y/y*)는 최소화하여 y/δ를 최대산출물이 되게 한다. 따라서 EIE는 다음과 같이 유도된다.
| (3) |
EIE의 분자의 y*는 최대산출량, W*는 최소오염량이다. y가 최대산출량이 되고 W가 최소오염량이 될 때 W*/y*는 최소 오염원단위가 될 수 있다. 식(3)을 전환하면 EIE는 환경효율과 생산효율을 곱한 것으로 정의한다(=θ×δ). 환경효율과 생산효율을 동시에 추정하는 방법으로 여기서는 Herrala and Goel(2012) 등이 사용한 비용함수 접근을 사용한다. 이러한 EIE의 동시추정모형은 비용함수를 이용하여 도출한다. 먼저 이를 위한 비용함수 형태의 초월대수 확률변경함수의 추정식은 다음과 같다.
| (4) |
이는 이산화탄소(CO2)배출량을 종속변수로 두고 자본스톡(K), 노동(L), 화석에너지(FF), 비화석에너지(NF), 산출량(y)을 설명변수로 둔 확률변경함수이다. u는 생산의 기술비효율오차이고 υ는 생산의 확률오차이다. 여기서 오염물은 최소화되어야 하므로 비용함수형태를 사용한 것이다. 확률변경비용의 형태이므로 식(4)에서 u가 음(-)이 아니라 양(+)으로 표시된 것이다. υ는 독립적이고 동일하게 로 분포한다. 환경원단위의 오차항(u)에 대한 분포가정은 단측 절단정규분포 (TND: truncated normal distribution)를 가정한다. 확률오차(υ)와는 독립적이고 임의의 점 μ를 기준으로 균등분포하지만 0에서 절단된 절단분포함수는 의 형태이다. 나아가 환경원단위 오차항이 분포가정에 따라서 변화하는지를 확인하기 위하여 환경비효율 오차(u)는 시간에 따라서 변화하는 형태를 가정할 것이다.
그런데 EIE를 도출하려면 오염물최소화의 환경효율이 구해져야 한다. 이를 위하여 생산비효율과 환경비효율이 모두 존재하지 않는 초월대수 확률변경함수가 필요하다. 이는 식(4)의 산출물에 최대산출물(y/δ)을 대입하고 환경비효율이 없도록 ui=0으로 두면 된다. 두 개의 비효율이 존재하지 않는 오염물 함수는 다음과 같다.
| (5) |
식(4)가 생산효율과 환경효율을 동시에 만족시키려면 식(5)와 동일하면 된다. 그러므로 다음 조건이 만족되면 두 효율은 동시에 만족된다. 즉,
| (6) |
여기서 lnδ의 1차항의 계수를 b라 두면 lnδ에 대한 근의 값은 다음과 같다.
| (7) |
식(4)를 추정하고 도출한 계수를 이용하여 식(7)에 대입하면 δ값을 도출할 수 있다. 이 δ값이 산출물의 생산효율이다. 식(4)의 exp(-u)는 환경효율이다. 여기서 구한 두 값을 이용하여 EIE를 도출할 수 있다.
Ⅲ.실증분석
1. 자료
실증에서는 166개 국가를 대상으로 1996-2018년기간 동안 자료를 사용한다.9) 산출변수인 부가가치로는 실질GDP를 사용하고 투입변수로는 자본스톡(K), 노동(L), 화석에너지소비(FF), 비화석에너지소비(NF), 오염물로는 이산화탄소(CO2)를 사용하였다.10) 노동은 종사자 수, 에너지소비량은 화석에너지와 비화석에너지로 구분하였다. 이와 같은 사항을 아래의 <표 1>에 제시하였다.
본 연구에서는 166개국을 1인당 GDP에 따라 5개의 국가그룹으로 구분하였다. 5개 국가그룹의 분류기준은 World Bank의 구분에 의한 소득수준이다 (2018년 회계년도 기준).11) 자세한 분류기준 및 그룹표기는 <표 2>와 같다. <표 2>에서 그룹별 소득기준과 국가수를 확인할 수 있다. 다음으로 <표 3>은 국가그룹별 실질GDP, 이산화탄소배출량, 자본스톡, 노동, 화석에너지소비량, 비화석에너지소비량, 원자력에너지소비량의 기초통계량을 보여준다.12)
2018년 실질GDP, 이산화탄소배출량, 자본스톡, 화석에너지소비량의 평균은 G1, G3, G4, G2, G5 순으로, 노동의 평균은 G4, G3, G1, G5, G2 순으로, 비화석에너지소비량은 G1, G3, G4, G5, G2 순으로 높다.13) 비화석에너지소비량에서 G2의 최솟값이 0인 것을 통해 비화석에너지 설비가 없는 국가도 존재함을 알 수 있다.14) 또한 G2, G5의 국가들은 모두 원자력이 없어서 최댓값이 0이고, 30개국만 원자력에너지를 소비하고 있다.
2. 실증결과
본 연구의 실증에서는 이론모형에서 제시한 확률변경 비용형태에 기초하여 CO2배출량에 대한 환경효율과 함께 산출물의 생산효율을 동시에 추정한다. 확률오차는 정규분포를 하고 환경비효율오차의 분포는 절단정규분포(truncated normal distribution)를 하는 것으로 가정한다. 나아가 환경비효율오차의 존재와 불변여부에 대한 가설검정과 초월대수함수에 대한 가설검정의 적합성을 확인한다.
먼저 이산화탄소의 환경효율을 추정한 초월대수 추정식은 <표 4>와 같다. 알려져 있듯이 효율을 측정하는 확률변경추정에서는 비효율오차의 분포형태에 따른 비효율의 존재가 중요하고 비효율의 시간에 따른 추이 등이 중요하다.
σ2, γ, μ, η 등이 모두 1% 유의수준에서 유의적으로 나타나서 추정식은 강건한 것으로 보인다. σ2는 오염비효율 오차항과 확률오차항의 분산으로서 이 분산은 두 오차항의 존재를 확인시켜준다. γ는 복합오차항의 분산에 대한 오염비효율오차항의 분산의 비율로 정의되고 그 값의 크기에 따라 전체 오차항 중 오염비효율오차항이 차지하는 비중이 된다. μ는 절단정규분포의 좌우 분포의 평균값으로서 μ가 유의적이면 평균이 0이 중심인 반정규분포(half normal distribution)가 아니라 μ를 중심으로 분포하는 것을 의미한다. η는 오염비효율이 시간에 따라서 변화하는 정도를 보여준다. γ는 0.885로 복합오차 가운데 약 88.5%가 환경비효율오차로 인한 것으로 나타났다. 또한 μ는 0.738로서 이를 중심으로 좌우가 대칭되는 분포를 하는 것으로 나타났다. 즉, 0.738의 수준에서 가장 많은 관측치가 집중되어 있고 그 점을 중심으로 관측치가 정규분포하는 것으로 나타났다. η는 0.005로 시간이 흐름에 따라서 환경효율이 개선되기는 하지만 매우 미미한 수준으로 연간 0.5% 수준에 불과하다.
다음으로 설명변수들과 종속변수인 CO2 배출량과 관계를 살펴보자. 노동, 화석에너지, 산출물 등은 1% 유의수준에서 유의적이고 정(+)의 부호를 보여준다. 즉, 노동과 화석에너지, 산출량 등이 증가하면 이산화탄소가 비례해서 증가한다. 세 변수 중 화석에너지의 추정계수가 0.795로 다른 변수보다도 이산화탄소 증가에 더 영향을 주는 것으로 나타나고 있다.
다음으로 본 연구에서 추정식에서 살펴본 결과가 가설검정에서도 지지되는지를 확인해볼 필요가 있다. 비효율성의 존재, 추정모형의 적합성에 관한 가설검정을 실시한 결과는 <표 5>와 같다.
가설검정은 환경비효율 오차의 존재 및 시간변화에 관한 모형의 적합성에 관한 것이다. 첫째, 환경비효율이 없고 비효율이 불변이라는 귀무가설은 OLS의 로그우도값이 –543.23이고 MLE의 로그우도값이 1561.33으로서 LR검정값이 4290.12이다. 이는 χ2분포의 임계값 9.21을 크게 벗어났기에 귀무가설은 기각되고 대립가설이 채택된다. 그러므로 환경비효율은 존재하고 시간에 따라 변화한다는 것이 검정되었다.
둘째, ‘추정함수모형으로 콥-더글러스 모형이 적합하다’는 귀무가설을 검정하였다. 콥-더글러스 모형의 MLE 로그우도값은 1422.26이고 초월대수모형의 MLE 로그우도값은 1561.33으로서 LR검정값은 278.13이다. LR검정값이 χ2분포의 임계값이 30.58을 초과하였으므로 귀무가설은 기각되고 대립가설이 채택된다. 즉, 추정모형은 콥-더글러스가 아니라 초월대수모형이 적합한 것으로 판정되었다.
이러한 결과에 의하면 환경 비효율오차는 존재하고 시간에 따라서 변화한다. 또한 추정함수는 콥-더글러스 함수보다는 초월대수함수가 적합하고 타당한 것이 확인되었다.
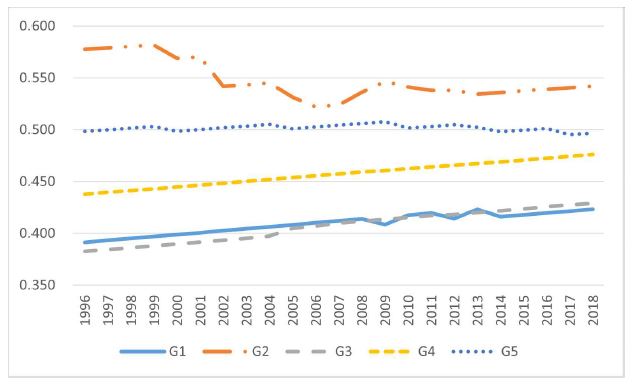
이어서 추정된 환경효율, 생산효율, 환경원단위 효율을 그림으로 제시하면 <그림 1>과 같다. 실제 관측치는 166개국이지만 이들을 모두 제시하기에는 지면의 한계가 있으므로 여기서는 5개 소득그룹으로 구분한 것이다. <그림 1>은 5개 소득그룹에 대한 이산화탄소에 대한 환경효율의 평균추이를 보여주고 있다. 첫째, 이산화탄소의 환경효율은 완만하지만 매년 평균 0.5%의 수준으로 향상되는 추이를 보여주고 있다. 5개 그룹으로 볼 때. 제조업이 없고 금융이나 무역이 발달하였거나 석유산유국들이 주로 속한 G2그룹의 효율이 가장 높다.15) 그 다음으로 소득수준이 낮은 G5그룹이나 G4그룹이 그 뒤를 따른다. G1그룹의 환경효율은 온실가스 저감에 가장 앞서 있지만 온실가스의 배출량이 절대적으로 많기때문에 상대적으로 낮다. 반면 G5그룹은 저개발상태로 온실가스배출량이 상대적으로 작아서 환경효율이 높게 나타난다.
둘째, 연도별 생산효율은 <그림 2>와 같다. <그림 2>에서 보는 바와 같이 환경효율과 같이 생산효율도 매년 일정하게 증가하는 형태를 보여준다. 그룹별로는 G2그룹의 효율이 가장 높고 그 다음으로 G1그룹이 따른다. 반대로 G3그룹과 G4그룹이 가장 낮고 오히려 G5그룹의 생산효율이 높다. 이는 G5그룹에서 주어진 실제 소득에 비하여 상대적으로 가능한 최대소득이 높지 않다는 것을 의미한다.
셋째, 환경원단위 효율은 <그림 3>과 같다. 환경원단위 효율은 일정하게 증가 추이를 보여준다. 이는 생산효율뿐만 아니라 환경효율이 일정하게 증가하는 추세를 보여주기 때문이다. 증가추세를 보인 것은 각국이 경제성장을 추구하는 가운데 온실가스 감축도 동시에 노력한 결과로 보인다.
EIE의 5개 그룹의 결과를 비교해 보면 G2그룹이 분석기간 동안 연평균 0.463으로서 가장 높았고 그 다음으로 G5그룹(0.400)으로 나타났다. G2그룹은 홍콩, 싱가포르 등 도시국가들과 중동의 산유국들로서 소득수준이 높지만 온실가스 배출이 작은 금융업, 무역업, 석유수출업 등으로 제조업이 없는 국가들로 구성되어 있다. G5는 이와 정반대로 저개발상태로 GDP도 낮지만 온실가스 배출도 낮아서 EIE가 높게 나타난 것으로 보인다.
이러한 그룹별 세 효율의 연평균치와 전통적 원단위(CO2/GDP)를 동시에 제시하면 <표 6>와 같다. G1그룹이 생산효율은 높지만 환경효율이 낮기 때문에 EIE는 아주 낮게 나타나고 있다. G3그룹과 G4그룹도 생산효율은 높지만 G1그룹과 비슷하게 환경효율이 낮아서 EIE는 낮게 나타났다. 반면 G2그룹은 생산효율과 환경효율이 가장 높아서 EIE가 높은 것을 확인할 수 있다. 마찬가지로 G5그룹도 생산효율이 낮은 편은 아니면서 환경효율이 높기 때문에 G2그룹과 비슷하게 EIE는 높은 것으로 나타났다.16)
이러한 EIE를 5개 소득그룹의 전통적 원단위와 비교해 보자. <표 6>은 EIE와 전통적 원단위를 분석기간 동안 평균한 값이다. 전통적 환경원단위는 낮을수록 효율적으로 간주하므로 EIE와 환경원단위의 순위는 일치되는 않는 것을 확인할 수 있다. 즉, 전통적 원단위가 가장 효율적인 그룹은 G5그룹, G4그룹, G1그룹으로 나타났고 G3그룹과 G2그룹이 낮은 효율수준을 보여주고 있다. 특히 G1그룹, G2그룹의 경우 EIE와 원단위의 순위가 가장 차이가 나는 것을 확인할 수 있다. CO2원단위가 보여주듯이 G1그룹의 경우, CO2 배출량이 많더라도 상대적으로 GDP가 높아서 원단위가 낮은 것으로 나타난다. 본 연구의 EIE를 기준으로 OECD그룹은 효율이 낮은 편에 속한다. 반면 G2그룹은 원단위에서는 좋지 못했으나 EIE에서는 가장 높은 효율을 보여준다. 그러므로 EIE을 동시에 사용하여 전통적 원단위 효율기준을 보완할 필요가 있다.
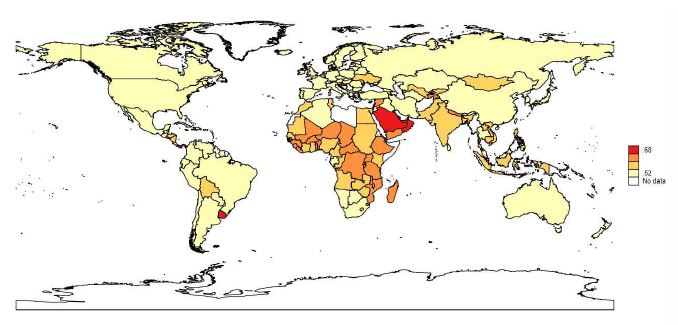
이와 같은 5개 그룹의 EIE의 분포를 세계지도를 가지고 표시하면 <그림 4>와 같다. <그림 4>에서 확인하듯이 G1그룹의 EIE는 낮게 나타났다. 반면에 주로 중동에 위치한 산유국들과 아시아에 속한 도시국가들이 가장 높은 수준을 보여주고 있다. 이어서 아프리카 국가들 및 아메리카의 일부 국가들이 그 다음으로 높은 것을 확인할 수 있다. 심지어 경제개발이 진행 중인 개도국들의 EIE보다 OECD 국가들의 EIE가 낮거나 비슷한 수준으로 나타난 것은 선진국 중심으로 주도되어 온 온실가스 저감노력이 아직도 성과를 더 높여야 할 여지가 있다. 즉, OECD 국가들은 빠른 경제성장으로 GDP 증가와 동시에 이산화탄소의 상응하는 증가가 있었고 이산화탄소 원단위는 낮아서 원단위를 개선할 여지는 다른 그룹보다 더 많이 남아 있다. 즉, 실증결과에 기초할 때, 지금까지 선진국들을 중심으로 이루어진 지속가능한 성장이란 목표가 국제적으로 잘 실현되고 있지 못한 것으로 보인다. 예를 들면, 미국, 독일, 일본, 한국 모두 G1그룹에 있고 이들 국가의 평균 EIE는 각각 0.330, 0.309, 0.354, 0.336로 G1그룹 평균값(0.319)의 주위에 모여 있다. 독일은 이미 1990년, 미국은 2005년, 일본은 2013년 탄소중립계획을 제시했다. 실증결과에 기초하면 이들 국가의 계획이 제대로 효과를 거두고 있는 것인지 의문이 든다. 한국은 온실가스 감축계획이 2017년에 제출되었고, 본 연구의 연구기간이 2018년까지이므로 이 기간 동안 평균 EIE는 낮은 수준이다. 즉, 한국의 EIE는 평균보다 낮은 상태이다.
이와 관련하여 환경원단위 효율과 탄소배출량, GDP, 전통적 환경원단위와의 관계에 대한 의문을 확인하고자 하였다. 즉, 본 연구에서는 추가적으로 이들 4 변수 간에 상관계수를 <표 7>과 같이 측정해 보았다. 온실가스 배출량이 많은 상위 20개 국가 중에서 환경원단위 효율이 높은 국가는 하나도 존재하지 않는다. 온실가스 배출량이 높으면 전통적 환경원단위는 당연히 나빠지게 되고 환경원단위 효율도 악화될 것으로 판단된다. 환경원단위 효율과 탄소배출량, GDP와의 각각 상관계수는 매우 낮아서 거의 관계가 없는 것을 확인할 수 있다. 이는 환경효율, 생산효율, EIE의 프런티어 형성에는 여러 투입물과 산출물이 동시에 포함되고 탄소배출량과 GDP는 그 중 한 요소일 뿐이라는 것을 보여준다. 반대로 EIE와 전통적 환경원단위는 평균 –0.596으로 상대적으로 높은 상관계수를 보였지만 완전상관인 1의 수준에서 보면 적지 않게 벗어난 것을 확인할 수 있다.
한편, 위에 제시한 5개 그룹의 평균은 국가별 사정을 다 반영하지 못하고 일관된 성향을 보여주지 못하는 점도 있다. 이처럼 국가들이 소득에 기준하여 상이한 그룹으로 분류되어 나타난 국가 간의 이질성 문제를 해결하고 동질적 그룹으로 재분류해 볼 필요가 있다. 즉, Zhang 등(2020)과 Kang and Kang(2022)가 도입한 평균-분산 분류접근법(Mean-Variance Classification Approach)을 사용하여 166개국을 5개의 소득그룹 대신에 4개의 유사한 그룹으로 재분류해 보았다. 이 4가지 그룹은 성숙(mature)그룹, 유망(promising)그룹, 고군분투(struggling)그룹, 부진(sluggish)그룹 등이다.
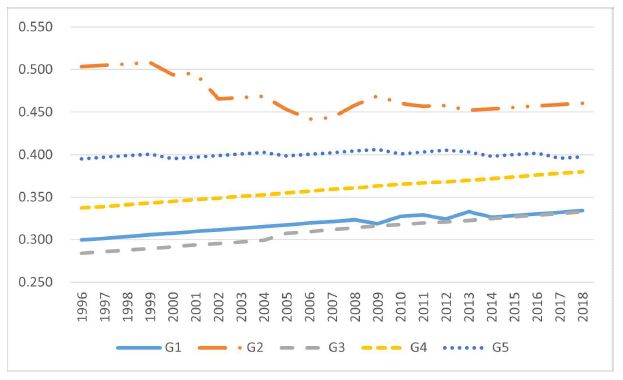
이러한 평균분산접근에 따라서 각 국가별 EIE의 평균과 분산의 중위수를 기반으로 4가지 형태의 그룹으로 재분류해 보았다. 166개 국가에 대한 EIE의 평균과 분산의 중위수는 각각 0.327과 0.0001789로 나타났다. 이를 바탕으로 평균값이 0.327 이상이고 분산이 0.0001789이하인 국가는 성숙그룹으로 분류하였다. 유망그룹은 EIE가 중위수 값 이상이고 분산이 중위수 값 이상인 국가이다. 반면, 고군분투그룹은 EIE의 평균이 0.327보다 작고 분산은 0.0001789보다 크다. 마지막으로, EIE 평균과 분산이 중위수 값보다 작은 국가는 부진그룹에 속한다. 이러한 4그룹에 속한 국가들의 EIE의 분포는 <그림 5>와 같다. 왼편의 5개의 소득그룹별 EIE에서는 그룹별 차이가 뚜렷하지 못했지만 오른편 그림의 4개 그룹에서는 EIE가 성숙그룹, 유망그룹, 고군분투그룹, 부진그룹 순서로 가시적으로 차이가 나고 있다.
소득에 기초하여 5개 그룹으로 분류한 166개 국가는 <표 8>과 같이 성숙국가 38개, 유망국가 47개, 고군분투국가 37개, 부진국가 44개로 분류되었다. <표 8>이 보여주듯이 일부 중간소득 및 저소득 국가 중에도 성숙그룹에 속한 국가가 있다. 이들 국가는 경제발전 수준이 낮고 이산화탄소 배출량도 적어서 EIE가 높은 것으로 보인다. 대부분의 G1 및 G2그룹 국가는 성숙하고 유망국가로 재분류되었다.
G1 및 G2 그룹에 속한 19개의 국가들이 성숙그룹에 속하고 이들은 지속적으로 높은 EIE를 보여준다.17) 이러한 성숙그룹은 다른 나라의 EIE를 개선하는 데 모범적인 사례가 될 수 있다. 유망그룹은 고군분투그룹보다 EIE가 높지만 동시에 변동 폭이 크기 때문에 빨리 성과가 높아지는 잠재력이 있다. 반면, 고군분투그룹은 평균값이 낮지만, 상대적으로 변동 폭이 크기 때문에 효율성 개선 가능성이 있다. 미국, 일본은 성숙그룹에 속하고 한국은 유망그룹에 속한다. 한국은 탄소중립 정책 제시가 늦고 탄소배출량 저감속도가 늦어서 더 많은 노력이 필요하다. 성숙그룹을 제외한 나머지 세 그룹에 속한 국가들은 앞으로 경제발전속에서 탄소배출은 아직 많이 미흡하여 탄소배출을 더 줄여야 하는 과제를 안고 있다.
Ⅳ. 결론
본 연구에서는 오염물 모형을 이용하여 환경효율과 생산효율에 기초한 EIE를 측정하여 보았다. 나아가 도출한 EIE를 전통적인 환경원단위와 비교하여 보았다. CO2 배출량 추정식에서 노동, 화석에너지, 산출물 등은 1% 유의수준에서 유의적이고 정(+)의 부호를 보여주었다. 세 변수 중 화석에너지의 추정계수가 0.795로 다른 변수보다도 CO2 배출량 증가에 크게 영향을 주는 것으로 나타났다. 환경 비효율오차는 존재하고 시간에 따라 변화하는 것으로 나타났다. 또한 추정함수는 초월대수함수가 보다 적합한 모형으로 검정되었다.
CO2 배출량에 대한 환경효율은 완만하지만 매년 평균 0.5%의 수준으로 향상되는 추이를 보여주고 있다. 환경효율은 고소득그룹(G2), 저소득국가(G5), 하위중간소득그룹(G4) 등의 순서로 높게 나타났다. 생산효율의 경우도 매년 일정하게 증가하는 형태를 보였는데 국가별로는 고소득그룹(G2)과 OECD그룹(G1)의 순서로 높았다. EIE도 완만하지만 매년 증가하는 형태를 보였다. 고소득그룹은 생산효율과 환경효율이 가장 높아서 EIE가 높았다. 반면 OECD그룹은 생산효율은 높지만, 환경효율이 매우 낮기 때문에 EIE는 매우 낮았다. 상위중간소득그룹(G3)과 하위중간그룹(G4)도 생산효율은 높지만, OECD와 비슷하게 환경효율이 낮아서 EIE는 낮게 나타났다. 오히려 저소득그룹(G5)은 EIE가 높았다. 이는 저소득국가가 환경효율은 높으면서 생산효율이 낮은 편이 아니었기에 나타난 현상이다.
이러한 EIE의 결과는 전통적 원단위에서 보여준 5개 그룹의 순위와는 많이 상이하였다. 전통적 원단위는 저소득그룹(G5), 하위소득그룹(G4), OECD그룹(G1) 순으로 높게 나타났다. 상위중간그룹(G3)과 고소득그룹(G2)이 낮은 효율수준을 보여주고 있다. 특히 OECD그룹의 경우 EIE와 원단위의 순위가 크게 차이가 나는 것을 확인할 수 있다. 유사하게 고소득국가그룹(G2)은 환경원단위에서는 낮았으나 EIE에서는 가장 높았다. 이는 고소득국가의 경우 소득에 비하여 CO2 배출량이 적지 않지만, 실제 CO2배출량이 거의 최소배출량에 근접되어 있기 때문에 환경효율이 가장 높았고 EIE가 가장 높게 나타난 것으로 보인다. OECD그룹의 결과에서 보듯이 전통적 환경원단위는 오염물이 많더라도 GDP가 크면 효율적으로 간주할 수 있기에 보완이 필요하다.
나아가 국가들이 상이한 그룹으로 분류되어 나타난 국가 간의 이질성을 동질그룹으로 전환하기 위하여 평균분산접근으로 재분류한 결과에 의하면 소득그룹별 EIE가 차이가 없던 결과가 그룹별로 가시적으로 원단위의 뚜렷한 차이를 보였다. 한국의 경우 EIE는 분석기간의 평균이 0.336로 전체 평균인 0.370보다 낮은 편에 속하였다. 이의 원인은 알려져 있듯이 한국이 화석에너지에 대한 의존도가 높고 산업구조가 중화학 공업의 비중이 높으며 에너지 다소비산업으로 구성비가 높기 때문에 GDP에 비하여 온실가스 배출량이 높기 때문인 것으로 보인다. 이미 주요 선진국들은 오래 전에 온실가스 저감계획을 실천하여 온실가스 배출이 시계열적으로 최고점을 지나서 감소패턴을 보이고 있다. 그러나 한국은 아직도 최고점에 이르지 못한 것으로 알려져 있다. 2021년에 2050탄소중립 계획을 수립하여 혁신적인 탄소저감계획을 발표하였으나 이를 실행하여 탄소중립으로 나아가기에는 30년이란 실행기간이 선진국에 비하면 매우 짧다. 향후 온실가스 저감계획을 추진하는 실행력이 한국의 EIE를 낮출 수 있는 관건이 될 것이다. 또한 이 탄소저감계획에서 GDP로 나타나는 경제성장이 어느 정도 제약을 받게 될 것인지도 중요하게 고려해야만 할 것이다. GDP 성장과 온실가스 저감은 동시에 추구되어야 할 하나의 과제로서 효율적인 탄소저감은 본 연구에서 제시한 EIE를 동시에 고려하면서 진행되어야 할 것이다.
본 연구의 실증결과를 통하여 얻게 되는 정책적 시사점은 첫째, EIE는 오염물을 최소화할 수 있는 저감가능성을 보여준다. 따라서 전통적 환경원단위보다는 보다 효율적으로 저감이 이루어지고 있는지를 보여줄 수 있다는 점에서 더 활용가능성이 높다. 둘째, 경제개발이 진행 중인 개도국들의 EIE보다 OECD 국가들의 EIE가 낮거나 비슷한 수준으로 나타난 것은 선진국 중심으로 주도된 온실가스 저감노력이 아직도 더 성과를 내야 할 것으로 보인다. 즉, 전통적 원단위는 지속적으로 개선을 보이지만 EIE는 개선해야할 여지가 많음을 보여주었다. 셋째, 저소득국가 등 소득이 낮은 국가들에서 EIE기준으로 효율이 낮은 편이 아니다. 하지만 경제개발의 속도가 빨라지게 되면 악화될 여지가 많으므로 이에 속한 국가들이 이산화탄소를 적게 배출하며 경제성장을 추구할 수 있는 성장경로를 찾을 필요가 있다.
본 연구의 한계점은 전반적으로 소득그룹에 따라서 경제발전의 단계가 상이할 것으로 본다면 경제발전의 산업기술에 차이가 있을 것이다. 이를 반영한 모형으로 기술격차를 고려한 메타 원단위 환경효율을 측정하고 그룹의 환경원단위 효율과 기술격차를 구분해서 측정하여 에너지전환과 환경규제에 따른 환경원단위의 변화에 대한 민감도를 측정할 필요가 있다. 이는 향후과제로 남긴다.
Acknowledgments
이 논문은 2021년 대한민국 교육부와 한국연구재단의 지원을 받아 수행된 연구임(NRF-2021S1A5A2A01069262).
References
-
강상목, 2017, “확률적 변경 초월대수함수를 이용한 대안적 에너지효율모델 개발과 국제적 비교,” 『환경정책』, 25(3), pp. 221~256.
[https://doi.org/10.15301/jepa.2017.25.3.221]

-
공지영・정수관・강상목, 2016, “확률변경비용함수를 이용한 환경오염지수 계측과 영향요인분석,” 『환경정책』, 24(3), pp. 207-231.
[https://doi.org/10.15301/jepa.2016.24.3.207]

-
김광욱・박혜란・강상목, 2011, “중국 29개 성의 환경성과 평가: 통합오염원 단위를 중심으로,” 『환경정책연구』, 10(1), pp.71-91.
[https://doi.org/10.17330/joep.10.1.201103.71]

-
김길환・노동운・이지웅, 2019, “확률적변경모형을 이용한 우리나라 기업의 온실가스배출효율성 추정,” 『한국기후변화학회지』, 10(2), pp. 117-128.
[https://doi.org/10.15531/KSCCR.2019.10.2.117]

- 김길환, 2020, “온실가스배출효율성에 미치는 상대적 온실가스배출량의 한계효과와 기업규모와의 관계에 대한 실증분석,” 『환경경영연구』, 12, pp. 1-24.
- 제러미 리프킨, 2012,『제3차 산업혁명』, (안진환 역), 서울: 민음사 (2011).
-
Aigner, D., C.A.K. Lovell, and P. Schmidt, 1977, “Formulation and estimation of stochastic frontier production function models,” Journal of Econometrics, 6(1), pp.21-37.
[https://doi.org/10.1016/0304-4076(77)90052-5]

-
Bibi, Z., Khan, D., and I.U. Haq, 2021, “Technical and Environmental Efficiency of Agriculture Sector in South Asia: a Stochastic Frontier Analysis Approach, “ Environment, Development and Sustainability, 23(6), pp.9260–9279.
[https://doi.org/10.1007/s10668-020-01023-2]

-
Bai,X., Salim,R., and Bloch,H., 2019, “ Environmental Efficiency of Apple Production in China: A Translog Stochastic Frontier Analysis,” Agricultural and Resource Economics Review, 48(2), pp. 199 – 220.
[https://doi.org/10.1017/age.2018.25]

-
Battese, G.E. and T.J. Coelli, 1992, “Frontier Production Function, Technical Efficiency and Panel Data: With Application to Paddy Farmers in India,” Journal of Productivity Analysis, 3(2), pp. 153-169.
[https://doi.org/10.1007/BF00158774]

-
Battese, G.E. and T. J. Coelli, 1995, “A Model for Technical Inefficiency Effects in a Stochastic Frontier Production Function for Panel Data,” Empirical Economics, 20(2), pp.325-332.
[https://doi.org/10.1007/BF01205442]

-
Chambers, R. G. and R.E. Just, 1989, “Estimating Multi-output Technologies,” American Journal of Agricultural Economics, 71(4), pp.880-995.
[https://doi.org/10.2307/1242674]

-
Cuesta R.A., Lovell, C.A.K., and J.L. Zofio, 2009, “Environmental Efficiency Measurement with Translog Distance Functions: A Parametric Approach,” Ecological Economics, 68(8), pp. 2232–2242.
[https://doi.org/10.1016/j.ecolecon.2009.02.001]

-
Duman, Y. S. and A. Kasman, 2018, “Environmental technical efficiency in EU member and candidate countries: A parametric hyperbolic distance function approach,” Energy, 147, pp.297-307.
[https://doi.org/10.1016/j.energy.2018.01.037]

-
Harrala R. and R.K. Goel, 2012, “Global CO2 Efficiency: Country-wise Estimates Using a Stochastic Cost Frontier,” Energy Policy, 45, pp.762-770.
[https://doi.org/10.1016/j.enpol.2012.03.007]

-
Hsiao, W., Hu, J., Hsiao, C., and M. Chang, 2019. “Energy Efficiency of the Baltic Sea Countries: an Application of Stochastic Frontier Analysis”. Energies, 12(1):104.
[https://doi.org/10.3390/en12010104]

-
Jondrow, J., Lovell, C.A.K., Materov, I.S., and P. Schmidt, 1982, “On the Estimation of Technical Inefficiency in the Stochastic Frontier Production Function Model,” Journal of Econometrics, 19(2), pp.233-238.
[https://doi.org/10.1016/0304-4076(82)90004-5]

-
Kang, M. and S. Kang, 2022, “ Energy Intensity Efficiency and The Effect of Changes in GDP and CO2 Emission,” Energy Efficiency, 15(8).
[https://doi.org/10.1007/s12053-021-10002-z]

-
Lansink, A.O. and E. Silva, 2003, “CO2 and Energy Efficiency of Different Heating Technologies in the Dutch Glasshouse Industry,” Environmental and Resource Economics, 24, pp.395-407.
[https://doi.org/10.1023/A:1023684316366]

-
Reinhard,S., Lovell, C.A.K. and G.J. Thijssen, 1999, “Econometric Estimation of Technical and Environmental Efficiency: An Application To Dutch Dairy Farms," American Journal of Agriculture Economics, 81(1), pp.44-60.
[https://doi.org/10.2307/1244449]

-
Reinhard, S., Lovell, C.A.K. and G.J. Thijssen, 2000, “Environmental Efficiency with Multiple Environmentally Detrimental Variables: Estimated with SFA and DEA,” European Journal of Operation Research, 121(2), pp.287-303.
[https://doi.org/10.1016/S0377-2217(99)00218-0]

-
Reinhard, S., Lovell, C.A.K. and G.J. Thijssen, 2002, “Analysis of Environmental Efficiency Variation,” American Journal of Agriculture Economics, 84(4), pp. 1054-1065.
[https://doi.org/10.1111/1467-8276.00053]

-
Zhang, H., Fan, L. W., and P. Zhou, 2020, “Handling Heterogeneity in Frontier Modeling of City-level Energy Efficiency: The Case of China. Applied Energy,” Applied Energy, 279, pp.1–10.
[https://doi.org/10.1016/j.apenergy.2020.115846]

-
Zhou, P., Ang, B.W., and D.Q. Zhou, 2012, “Measuring Economy-wide Energy Efficiency Performance: A Parametric Frontier Approach.” Applied Energy, 90(1), pp.196-200.
[https://doi.org/10.1016/j.apenergy.2011.02.025]

-
Zhou, Y., Zhang, X., Tian, X., Geng, X., Zhang, P., and B.Yan, 2015, “Technical and Environmental Efficiency of Hog Production in China-A Stochastic Frontier Production Function Analysis,“ Journal of Integrative Agriculture, 14(6), pp.1069–1080.
[https://doi.org/10.1016/S2095-3119(14)60990-4]

강상목: 부산대학교 경제통상대학 경제학부 교수로 재직중이다. 연구 관심분야는 환경규제, 환경지수, 지속가능성성장, 환경생산성 등이다. 주요 발표 논문은 다음과 같다. “An empirical study on effective pollution enforcement in Korea” (Environment and Development Economics, 2004), "A sensitivity analysis of Korean composite environmental index (CEI)" (Ecological Economics, 2002)(smkang@pusan.ac.kr).
리즈야오: 부산대학교 대학원 경제학부 박사수료과정으로 재학중이다. 연구 관심분야는 효율성과 생산성경제학, 환경경제학이다. (liziyao3721@hotmail.com)